
Quantitative Aptitude दैनिक क्विझ मराठीमध्ये: 21 जून 2021
IBPS RRB च्या परीक्षांसाठी Quantitative Aptitude आणि Reasoning या विषयात चांगले गूण मिळवण्यासाठी जास्तीत जास्त सराव करणे खूप गरजेचे असते. तर चला Quantitative Aptitude बद्दल तुमची तयारी तपासण्यासाठी खालील 21 जून 2021 ची Quantitative Aptitude ची दैनिक क्विझ पहा.
Subject: Quadratic Inequalities
Directions (1-5): या प्रत्येक प्रश्नात दोन समीकरणे (I) आणि (II) दिली जातात. आपल्याला दोन्ही
समीकरणे सोडवायची आहेत आणि उत्तर द्यावे लागेल
(a) जर x>y
(b) जर x≥y
(c) जर x<y
(d) जर x ≤y
(e) जर x = y किंवा x आणि y दरम्यान कोणताही संबंध स्थापित केला जाऊ शकत नाही
Q1. I. 6x² + 11x – 35 = 0
II. 2y² + 15y + 28 = 0
Q2. I. x² – 17x = 0
II. y³ – 4913 = 0
Q3. I. (x – 5)² – 100 = 0
II. y² + 16y = 5(y – 6)
Q4. I. 11x² + 18x + 7 = 0
II. 22y² + 25y + 7 = 0
Q5. I. 8x + 7y = 38
II. 3x – 5y = –1
Direction (6 – 10): खालील क्रमांक मालिकेत प्रश्नाच्या ठिकाणी काय येईल (?)खालील क्रमांक मालिकेत
प्रश्नाच्या ठिकाणी काय येईल (?):
Q6. 180, 185, 193, 207, 233, ?
(a) 268
(b) 278
(c) 273
(d) 295
(e) 283
Q7. 160, 82, 84, 128, ?, 647
(a) 342
(b) 314
(c) 292
(d) 258
(e) 284
Q8. ?, 334, 166, 82, 40, 19
(a) 570
(b) 558
(c) 670
(d) 640
(e) 645
Q9. 1250, 961, 736, 567, 446, ?
(a) 365
(b) 385
(c) 280
(d) 340
(e) 345
Q10. 120, 120, 126, 146, 188, ?
(a) 240
(b) 220
(c) 225
(d) 275
(e) 260
To Attempt the Quiz on APP with Timings & All India Rank, Download the app now, Click here
महाराष्ट्र राज्यातील सर्व स्पर्धा परीक्षांचे मोफत अभ्यास साहित्य
Adda247 मराठी App | Add247Marathi Telegram group
YouTube channel- Adda247 Marathi
Solutions
S1. Ans.(b)
Sol.
I. 6x² + 11x – 35 = 0
⇒ 6x² + 21x – 10x – 35= 0
⇒ 3x (2x + 7) – 5 (2x + 7) = 0
⇒ (3x – 5) (2x + 7) = 0
x = 5/3 , x = (–7)/2
II. 2y² + 15y + 28 = 0
⇒ 2y² + 8y + 7y + 28 = 0
⇒ 2y (y + 4) + 7 (y + 4) = 0
⇒ (2y + 7) (y + 4) = 0
y = (–7)/2, y = –4
∴x≥ y
S2. Ans.(d)
Sol.
I. x² – 17x = 0
⇒ x (x – 17) = 0
⇒ x = 0 or 17.
II. y³ – 4913 = 0
⇒ y = ∛4913 = 17
∴y ≥ x
S3. Ans.(b)
Sol.
I. (x – 5)² – 100 = 0
⇒ x² – 10x + 25 – 100 = 0
⇒ x² – 10x – 75 = 0
⇒ x² – 15x + 5x – 75 = 0
⇒ (x – 15) (x + 15) = 0
x = 15 , x = –5
II. y² + 16y = 5(y – 6)
⇒ y² + 16y – 5y + 30 = 0
⇒ y² + 11y + 30 = 0
⇒ y² + 6y + 5y + 30 = 0
⇒ (y + 6) (y + 5) = 0
y = –6, y = –5
∴x ≥ y
S4. Ans.(d)
Sol.
I. 11x² + 18x + 7 = 0
⇒ 11x² + 11x + 7x + 7 = 0
⇒ (11x + 7) (x + 1) = 0
x = (–7)/11, x = –1
II. 22y² + 25y + 7 = 0
⇒ 22y² + 14y + 11y + 7 = 0
⇒ 2y (11y + 7) + 1 (11y + 7) = 0
⇒ (2y + 1) (11y + 7) = 0
y = (–1)/2 , y=(–7)/11
∴y ≥ x
S5. Ans.(a)
Sol.
8x+7y=38
3x –5y= –1
Multiply 1st equation by 5 and 2nd equation by 7 and add both.
▁(■(40x+35y=190@21x – 35y= –7))
61x = 183
⇒ x = 3
Put x = 3 in 2nd equation.
⇒ 9 – 5y = –1
⇒ 5y = 10
⇒ y = 2
∴ x > y
S6. Ans.(e)
Sol.
S7. Ans.(d)
Sol.
S8. Ans.(c)
Sol.
Pattern is
670/2-1=334
334/2-1=166
166/2-1=82
82/2-1=40
40/2-1=19
? = 670
S9. Ans.(a)
Sol.
Pattern is,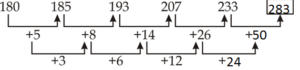
S10. Ans.(e)
Sol.
Pattern is,![]()








