Table of Contents
घनाकृती ठोकळे
फासे आणि घन (Dice and Cube) हा तर्कक्षमता विषयातील एक मनोरंजक आणि मूलभूत विषय आहे. यात दोन त्रिमितीय वस्तूंचा अभ्यास केला जातो. फासे आणि घनाकृती ठोकळे या वस्तू आपल्या तार्किक विचार आणि व्हिज्युअलायझेशन क्षमता वाढविण्यासाठी आकर्षक साधने म्हणून काम करतात. या विषयामध्ये, आम्ही कोडी, खेळ आणि विविध स्पर्धा परीक्षांमध्ये मोठ्या प्रमाणावर वापरले जाणारे फासे आणि घन यांचे गुणधर्म आणि वैशिष्ट्ये पाहुयात. या वस्तूंची मूलभूत तत्त्वे समजून घेतल्याने आपल्याला फासे आणि घन (Dice and Cube) या टॉपिक चे प्रश्न अगदी सरळ आणि सोप्या पद्धतीने सोडवता येतील. चला मग या लेखात आपण घनाकृती ठोकळे, व्याख्या, संकल्पना आणि महत्त्वाचे प्रश्न पाहुयात.

फासे आणि घन: विहंगावलोकन
या लेखाच्या शेवटी, तुम्हाला फासे आणि क्यूब्सच्या जगात मौल्यवान अंतर्दृष्टी प्राप्त झाली असेल, तुम्हाला तर्कसंगत आव्हानांचा आत्मविश्वासाने आणि सहजतेने सामना करण्यास सक्षम बनवेल. चला या शोधाच्या प्रवासाला सुरुवात करूया आणि खाली तक्त्यात फासे आणि घन (Dice and Cube) बद्दल विहंगावलोकन तपासा
| घनाकृती ठोकळे | |
| श्रेणी | अभ्यास साहित्य |
| साठी उपयुक्त | आदिवासी विकास विभाग भरती 2023 |
| विषय | तर्कशास्त्र |
| लेखाचे नाव | घनाकृती ठोकळे |
घनाकृती ठोकळे: व्याख्या, आणि संकल्पना
फासा (Dice): फासे लहान, फेकता येण्याजोग्या वस्तू असतात ज्या सामान्यत: विविध खेळ आणि जुगाराच्या क्रियाकलापांमध्ये वापरल्या जातात. ते सामान्यतः घनाकृती आकारात असतात ज्याचे पृष्ठे 1 ते विशिष्ट संख्येपर्यंत (बहुतेकदा 6) असतात.
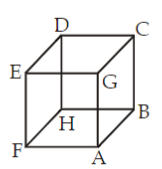
फासे एक घन आहे. घन मध्ये 6 पृष्ठे आहेत. घनामध्ये 6 पृष्ठे आहेत – ABCG, GCDE, DEFH, BCDH, AGEF आणि ABHF. नेहमी चार पृष्ठे एका पृष्ठाला लागून असतात. येथे CDEG हा क्यूबचा वरचा पृष्ठ आहे आणि ABHF हा क्यूबचा खालचा पृष्ठ आहे.
फासेचे प्रकार (Types of Dice)
फासे दोन प्रकारचे असतात ते म्हणजे साधे फासे (Simple Dice) आणि मानक फासे (Standard Dice).
साधे फासे (Simple Dice)
साधे फासे (Simple Dice): साध्या फासेमध्ये, विरुद्ध बाजूच्या पृष्ठाच्या संख्येची बेरीज सात नसते. याचा अर्थ कोणत्याही दोन समीप बाजूंची बेरीज 7 असते.
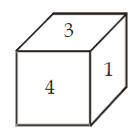
येथे, 3 + 4 = 7, तर हे साधे फासे आहे.
मानक फासे (Standard Dice): मानक फासे मध्ये, दोन विरुद्ध बाजूंची बेरीज सात असते. याचाच अर्थ कोणत्याही दोन लगतची बेरीज सात नसते.
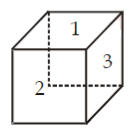
आकृतीवरून; आकृतीवरून; 1 + 2 = 3, 2 + 3 = 5, 3 + 1 = 4 म्हणजेच बेरीज सात नाही. म्हणून, आपण असे म्हणू शकतो की विरुद्ध बाजूंच्या संख्येची बेरीज सात असणे आवश्यक आहे. मानक फासे मध्ये: 1, 6 च्या विरुद्ध असेल, 2, 5 च्या विरुद्ध असेल, 3, 4 च्या विरुद्ध असेल.
घनाकृती ठोकळे: काही महत्त्वाचे नियम
काही महत्त्वाचे नियम खालीलप्रमाणे आहेत:
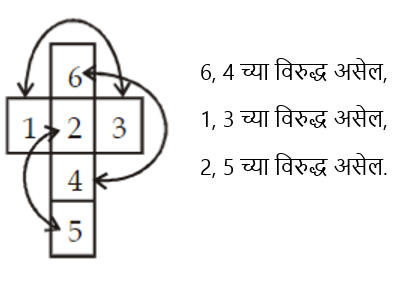
- जेव्हा फास्यांच्या दोन भिन्न स्थानांची संख्या भिन्न असते तेव्हा ते एकमेकांच्या विरुद्ध असतात.

- जर दिलेल्या दोन फास्यांची एक बाजू समान स्थितीत समान असेल तर उर्वरित एकमेकांच्या विरुद्ध असतील.
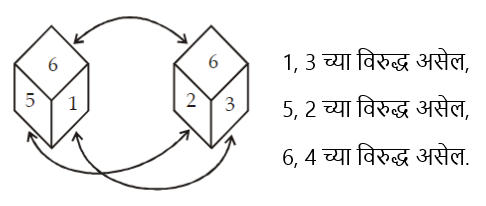
- जर दिलेल्या फासाच्या दोन बाजू समान स्थितीत सामायिक असतील, तर उर्वरित भाग एकमेकांच्या विरुद्ध असतील.
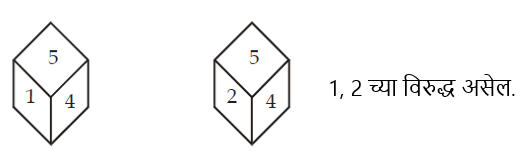
- घनाकृती ठोकल्याचे विस्तारित स्वरूप (Expanded form of Dice)
घनाकृती ठोकळ्यांवर काही महत्वाचे प्रश्न
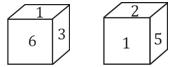
Q1. एकाच फासाची दोन स्थिति दिल्या आहेत. ‘6’ तळाशी असल्यास कोणती संख्या सर्वात वर असेल?
(a) 1
(b) 2
(c) 5
(d) 3
Q2. दिलेली प्रश्न आकृती दुमडल्यावर तयार होणारा घन निवडा.
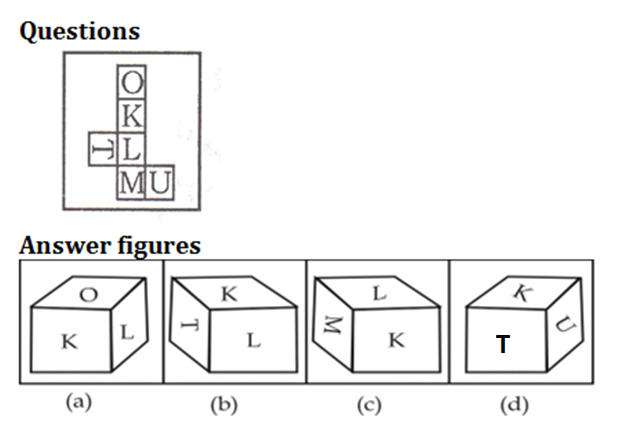
(a) a
(b) b
(c) c
(d) d
Q3. घनाची तीन स्थिति दिल्या आहेत. त्यांच्या आधारावर दिलेल्या घनमध्ये कोणत्या संख्या, संख्या 2 च्या विरुद्ध बाजूस असेल?
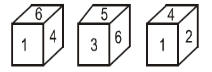
(a)2
(b) 5
(c) 1
(d) 6
Q4. एकाच फासाच्या दोन स्थिती दिल्या आहेत. ‘1’ शीर्षस्थानी असल्यास कोणती संख्या तळाशी असेल?
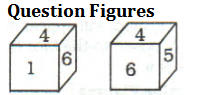
(a) 6
(b) 5
(c) 4
(d) 2
Q5. खाली एकाच फासाच्या दोन स्थिती दिल्या आहेत. जर 3 तळाशी असेल, तर कोणती संख्या शीर्षस्थानी असेल ?
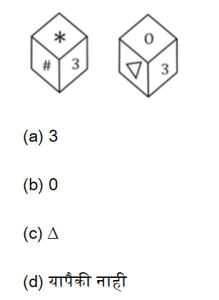
Q6. एका फासाच्या चार स्थिति खाली दिल्या आहेत. जेव्हा शीर्षस्थानी 1 असेल तेव्हा तळाशी कोणती संख्या असेल ते ओळखा.
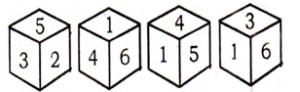
(a) 6
(b) 3
(c) 2
(d) 5
Q7. एकाच फासाची दोन स्थिती दिल्या आहेत. ‘5’ खाली असल्यास कोणती संख्या सर्वात वर असेल?
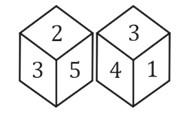
(a) 2
(b) 6
(c) 4
(d) 1
Q8. एकाच फासाचे वेगवेगळे स्थान दाखवले आहे. तळाशी असलेल्या चार ठिपक्यांच्या वरच्या बाजूला किती ठिपके असतील?
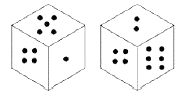
(a) 3
(b) 2
(c) 1
(d) 5
Q9. फासाच्या दोन स्थिती दिल्या आहेत. 5 च्या विरुद्ध कोणती संख्या असेल?
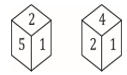
(a) 3
(b) 2
(c) 1
(d) 4
Q10. एकाच फासाच्या वेगवेगळ्या स्थिती दिल्या आहेत. 2 च्या विरुद्ध बाजूवर कोणती संख्या असेल?
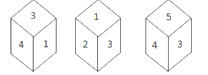
(a) 4
(b) 5
(c) 3
(d) 6
S1. Ans (c)
3, 2 च्या विरुद्ध असेल
6, 5 च्या विरुद्ध असेल
S2. Ans.(b)
S3. Ans. (d)
Sol.
6 चा समीप पृष्ठे आहेत- 1,3,4,5. त्यामुळे 2 विरुद्ध बाजूस आहे.
S4. Ans. (b):
Sol. जेव्हा 6 आणि 4 दोन्ही घनाच्या समान स्थितीत असतात, तेव्हा 5 हे 1 च्या विरुद्ध असले पाहिजे.
S5. Ans.(d)
Sol. O आणि ∆ हे 3 च्या शेजारी असतील त्यामुळे ते 3 च्या विरुद्ध असू शकत नाहीत
S6. Ans. (c)
Sol. विरुद्ध पृष्ठे 56, 34 आणि 21 आहेत.
S7. Ans.(c)
Sol.
| 3 | 2 | 5 |
| 3 | 1 | 4 |
3 → 6
2 → 1
5 → 4
S8. Ans.(a)
Sol.

4 ठिपके तळाशी असल्यास शीर्षस्थानी 3 ठिपके असतील
S9. Ans.(d)
Sol. 4
S10. Ans.(a)
Sol. 3 – 2 – 1
3 – 4 – 5
Note: महाराष्ट्रातील सर्व स्पर्धा परीक्षांसाठी ऑनलाईन क्लास, व्हिडिओ कोर्स, टेस्ट सिरीज, पुस्तके आणि इतर अभ्यास साहित्य खाली दिलेल्या लिंक वर क्लिक करून मिळवा.
Maharashtra Exam Study Material
अड्डा 247 मराठी अँप | अड्डा 247 मराठी टेलिग्राम ग्रुप




