Table of Contents
विभाज्यतेच्या कसोट्या (Divisibility Rules)
आदिवासी विकास विभाग भरती 2023 साठी अंकगणित हा अतिशय महत्त्वाचा विभाग आहे आणि केंद्र किंवा राज्य सरकारद्वारे घेतल्या जाणाऱ्या इतर सर्व परीक्षांमध्ये याला अधिक महत्त्व आहे. यात साधारणपणे, मूलभूत संकल्पना, विभाज्यता नियमातील तथ्यांशी संबंधित प्रश्न विचारले जातात. तर चला या लेखात आपण सर्व विभाज्यतेच्या कसोट्या पाहुयात.
विभाज्यतेच्या कसोट्या (Divisibility Rules): विहंगावलोकन
तुम्हाला गणित विभागाचा अधिकाधिक फायदा घेता यावा यासाठी आम्ही विभाज्यता नियमाशी संबंधित महत्त्वाची तथ्ये देत आहोत. आगामी आदिवासी विकास विभाग भरती 2023 साठी विभाज्यतेच्या कसोट्या (Divisibility Rules) वर आधारित प्रश्न सोडवण्यासाठी आवश्यक सर्व माहिती खाली या लेखात दिले आहे. खालील तक्त्यात आपण विभाज्यतेच्या कसोट्या (Divisibility Rules) बद्दल विहंगावलोकन पाहू शकता.
| विभाज्यतेच्या कसोट्या (Divisibility Rules): विहंगावलोकन | |
| श्रेणी | अभ्यास साहित्य |
| उपयोगिता | आदिवासी विकास विभाग भरती 2023 साठी व इतर सर्व स्पर्धा परीक्षांसाठी |
| विषय | अंकगणित |
| टॉपिकचे नाव | विभाज्यतेच्या कसोट्या (Divisibility Rules) |
| लेखातील प्रमुख मुद्दे |
|
विभाज्यतेच्या कसोट्या (Divisibility Rules)
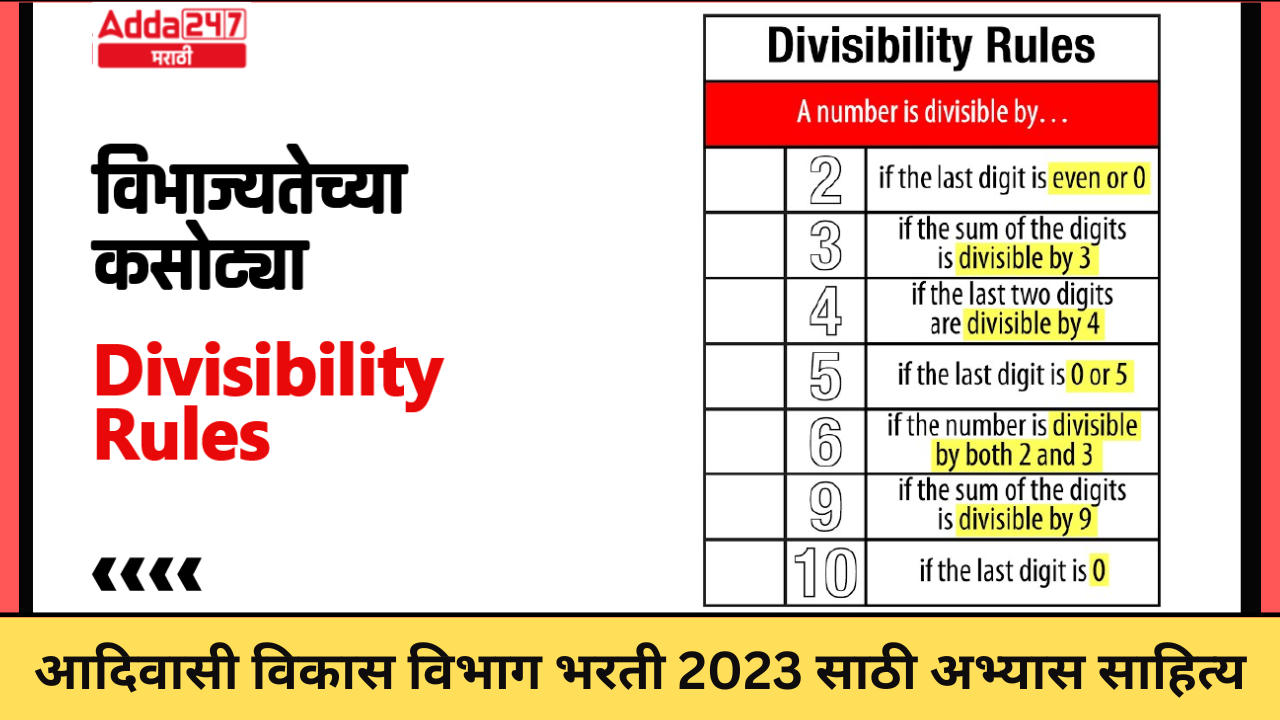
- 2 ने विभाज्यता → जर संख्येचा शेवटचा अंक 2 ने भागत असेल
उदा .: 92, 76, 112 यांना 2 ने भाग जातो
- 3 ची विभाज्यता → अशा सर्व संख्या ज्यांच्या अंकांची बेरीज 3 ने भाग जाते
- 4 ने विभाज्यता → जर संख्येचे शेवटचे दोन अंक 4 ने भागले तर
उदा. : 6316 ही संख्या घ्या. शेवटचे दोन अंक 16 विचारात घ्या. जसे 16 ला 4 ने भाग जातो, त्याचप्रमाणे मूळ संख्या 6316 ला देखील 4 ने भाग जातो.
- 5 ने विभाज्यता → शेवटचा अंक (0 आणि 5) 5 ने भागल्यास
उदा.: 100, 195, 118975 यांना 5 ने भाग जातो
- 6 ने विभाज्यता → जर एखाद्या संख्येला 2 आणि 3 ने निःशेष भाग जात असेल तर त्या संख्येला 6 ने निःशेष भाग जातो
उदा.: 834, शेवटचा अंक 4 असल्याने संख्या 2 ने निःशेष भाग जाते. अंकांची बेरीज 8+3+4 = 15 आहे, ज्याला 3 ने भाग जातो. त्यामुळे 834 ला 6 ने भाग जातो.
- 7 ने विभाज्यता → शेवटचा अंक दुप्पट करा आणि उर्वरित अग्रगण्य संख्येमधून वजा करा. जर निकालाला 7 ने भाग जात असेल तर मूळ संख्येला 7 ने निःशेष भाग जाईल.
- 8 ने विभाज्यता → जर संख्येचे शेवटचे तीन अंक 8 ने भागले तर
- 9 ची विभाज्यता → अशा सर्व संख्या ज्यांच्या अंकांची बेरीज 9 ने भाग जाते
- 11 ने विभाज्यता → विषम स्थानी असलेल्या अंकांची बेरीज आणि सम स्थानांमधील अंकांची बेरीज यांचा फरक ‘0’ किंवा 11 चा गुणाकार असेल तर त्या संख्येला 11 ने निःशेष भाग जाईल.
- 16 ने विभाज्यता → जर संख्येचे शेवटचे चार अंक 16 ने भागले तर
- 25 ने विभाज्यता → जर संख्येचे शेवटचे दोन अंक 25 ने भागले तर
- 32 ने विभाज्यता → जर संख्येचे शेवटचे पाच अंक 32 ने भागले तर
- 125 ने विभाज्यता → जर संख्येचे शेवटचे तीन अंक 125 ने भाग जात असतील तर
- 3, 7, 11, 13, 21, 37 आणि 1001 ने विभाज्यता →
(i) अंक 6 वेळा पुनरावृत्ती करून कोणतीही संख्या बनविल्यास ती संख्या 3, 7, 11, 13, 21, 37 आणि 1001 इत्यादींनी भाग जाईल.
(ii) तीन अंकी संख्येची पुनरावृत्ती करून सहा अंकी संख्या तयार केली तर; उदाहरणार्थ, 256, 256 किंवा 678, 678 इ. या फॉर्मची कोणतीही संख्या नेहमी 7, 11, 13, 1001 इ. ने पूर्ण भाग जाते.
विभाज्यतेच्या कसोट्या काही महत्त्वाचे मुद्दे
- a ला जर b ने भाग जात असेल, तर ac ला देखील b ने भाग जाईल.
- a ला जर b ने भाग जात असेल, आणि b ला c ने भाग जात असेल, तर a हा c ने निःशेष भाग जाईल.
- जर n ला d ने भाग जात असेल आणि m ला d ने भाग जात असेल तर (m + n) आणि (m-n) हे दोन्ही d ने निःशेष भाग जातील. याचा एक महत्त्वाचा अर्थ आहे. समजा 48 आणि 528 हे दोन्ही 8 ने निःशेष भाग जात आहेत. तर (528 + 48) तसेच (528 – 48) यांना 8 ने भाग जातो.
Note: महाराष्ट्रातील सर्व स्पर्धा परीक्षांसाठी ऑनलाईन क्लास, व्हिडिओ कोर्स, टेस्ट सिरीज, पुस्तके आणि इतर अभ्यास साहित्य खाली दिलेल्या लिंक वर क्लिक करून मिळवा.
Maharashtra Exam Study Material
अड्डा 247 मराठी अँप | अड्डा 247 मराठी टेलिग्राम ग्रुप