Correct option is B
The sum of the eigenvalues of the matrix is
If and , then value of is
if are three unequal numbers and then is
The product of the cofactors of 3 and -2 in the matrix is:
 is equal to:
is equal to:
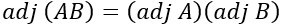
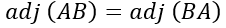
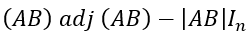 is a null matrix of order n.
is a null matrix of order n.


