Correct option is A
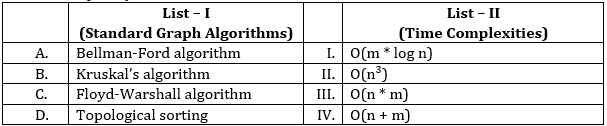
In question it is asked to match standard graph algorithms with their respective time complexities. Below is the detailed breakdown:
Bellman-Ford Algorithm:
· Used for single-source shortest path finding, even with negative weight edges.
· Time complexity: O(n ⋅ m), where n is the number of vertices and m is the number of edges.
Kruskal's Algorithm:
· Used to find the minimum spanning tree in a weighted graph.
· Time complexity: O(m ⋅ log n), as it involves sorting the edges and applying union-find operations.
Floyd-Warshall Algorithm:
· Used for finding shortest paths between all pairs of vertices in a weighted graph.
· Time complexity: O(n3), since it iterates over all vertex pairs multiple times.
Topological Sorting:
· Used to linearly order vertices of a Directed Acyclic Graph (DAG).
· Time complexity: O(n + m), as it involves visiting all vertices and edges once in a DFS or Kahn's Algorithm.
Final Matching:
A. Bellman-Ford Algorithm - III. O(n ⋅ m)
B. Kruskal's Algorithm - I. O(m ⋅ log n)
C. Floyd-Warshall Algorithm - II. O(n3)
D. Topological Sorting - IV. O(n + m)
Information Booster:
1.
Bellman-Ford Algorithm:
· Works even with negative weight edges.
· Detects negative weight cycles.
2.
Kruskal’s Algorithm:
· Greedy algorithm.
· Efficient when edges are significantly fewer than vertices.
3.
Floyd-Warshall Algorithm:
· Dynamic Programming-based algorithm.
· Inefficient for large graphs due to cubic complexity.
4.
Topological Sorting:
· Linear ordering of DAG nodes.
· Useful in task scheduling problems.
Additional Knowledge:
· O(n ⋅ m) is typical for graph traversal algorithms like Bellman-Ford.
· Algorithms like Kruskal benefit from efficient edge sorting, hence O(m ⋅ log n).
· O(n3) algorithms, such as Floyd-Warshall, are infeasible for very large graphs.
· DAG-based algorithms, including topological sort, are usually O(n + m).
