Given figure shows velocity-time graph of a ball of mass 250g rolling on a concretefloor. Compute the acceleration and the frictional force of the floor on the ball?

Correct option is B

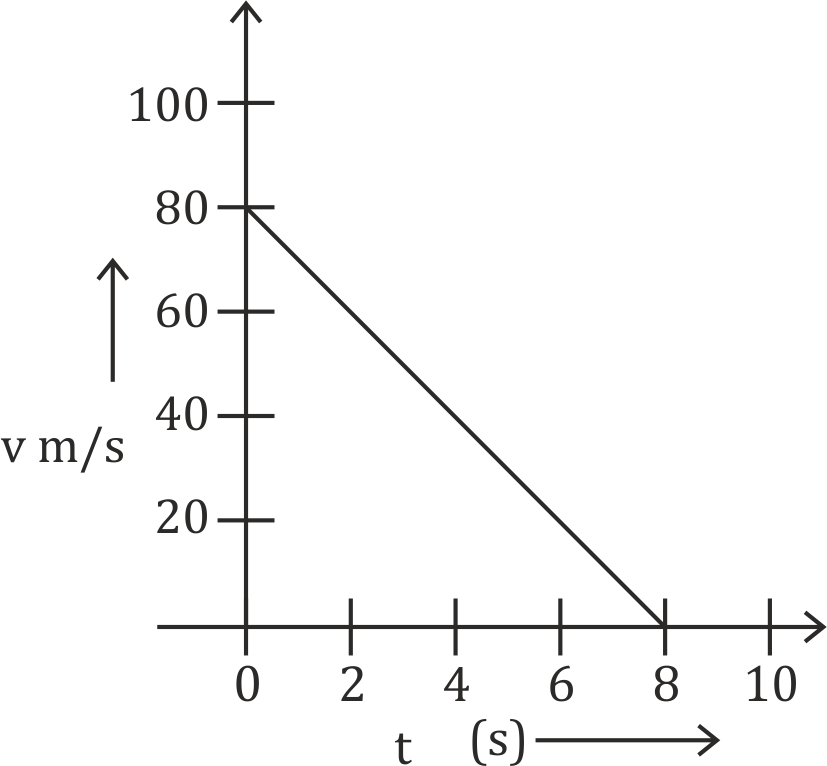
​$$\textbf{Given:} \\\quad \bullet\ \text{Mass of the ball, } m = 250\, \text{g} = 0.25\, \text{kg} \\\quad \bullet\ \text{Initial velocity, } v_1 = 80\, \text{m/s} \\\quad \bullet\ \text{Final velocity, } v_2 = 0\, \text{m/s} \\\quad \bullet\ \text{Time taken, } t = 8\, \text{s} \\\\\textbf{Concept:} \\\quad \bullet\ \text{The slope of a velocity-time graph gives acceleration.} \\\quad \bullet\ \text{The force of friction is calculated using Newton's second law:} \\\quad \quad f = m \cdot a$$

$$\quad a = \frac{v_2 - v_1}{t} = \frac{0 - 80}{8} = -10\, \text{m/s}^2 \\\\\quad f = m \cdot a = 0.25 \cdot (-10) = -2.5\, \text{N}$$​​​