Given below are two statements:
Statement I: The family of context-free languages is closed under homomorphism.
Statement II: The family of context-free languages is closed under reversal.
In light of the above statements, choose the correct answer from the options given below:

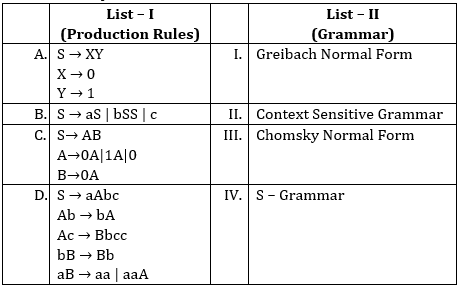
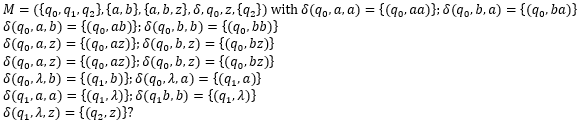Correct option is A

Statement I: The family of context-free languages is closed under homomorphism
(True)
Homomorphism is a mapping of input symbols to strings (e.g., mapping a → xy, b → z, etc.). For any context-free language L, applying a homomorphism h (where each symbol in L is replaced by its image under h) results in another context-free language. This is because the transformation can be modelled by modifying the production rules of the grammar.
Statement II: The family of context-free languages is closed under reversal (True)
Reversal means reversing the strings of the language (e.g., abc → cba). For a context-free language L, if we construct a grammar where each production rule generates strings in reverse order, the reversed language is also context-free. Hence, context-free languages are closed under reversal.
Information Booster:
· Closure Properties of Context-Free Languages (CFL):
1. Closed under: Union, concatenation, Kleene star, reversal, and homomorphism.
2. Not closed under: Intersection, complementation, and difference.