Preparing for the Odisha Teacher Eligibility Test (OTET) Paper-I requires a strong grasp of mathematics concepts relevant to the secondary school curriculum. Here, we present a curated selection of 30 multiple-choice questions (MCQs) covering various topics in mathematics. These questions are designed to help you assess and reinforce your understanding in preparation for the exam.
Top 30 Mathematics MCQS For OTET Paper-I Exam
- What is the primary study of mathematics?
(a) History
(b) Language
(c) Numbers, space, direction, and measurement
(d) Music
Ans. (c) Numbers, space, direction, and measurement - Which of the following statements best describes mathematical knowledge?
(a) It is often forgotten once accepted
(b) It is systematic, logical, and clearer
(c) It is based on opinions and beliefs
(d) It is ambiguous and vague
Ans. (b) It is systematic, logical, and clearer - Mathematics is crucial in fostering which of the following mindsets in children?
(a) Artistic
(b) Scientific and healthy
(c) Historical
(d) Literary
Ans. (b) Scientific and healthy - In mathematics, how are abstract notions handled?
(a) They are ignored
(b) They are translated into tangible forms
(c) They are only theoretical and never practical
(d) They are simplified into basic concepts only
Ans. (b) They are translated into tangible forms - Which field is NOT directly associated with the application of mathematics?
(a) Biology
(b) Chemistry
(c) Literature
(d) Physics
Ans. (c) Literature - Which of the following statements best describes the behaviorist approach to teaching Mathematics?
(a) Emphasizes active engagement and problem-solving
(b) Focuses on rote memorization and direct instruction
(c) Encourages collaboration and inquiry-based learning
(d) Believes knowledge is constructed by the learner
Answer: (b) Focuses on rote memorization and direct instruction - Who were the two major proponents of behaviorism in education?
(a) Piaget and Vygotsky
(b) Skinner and Watson
(c) Jones and Brader-Araje
(d) Skinner and Piaget
Answer: (b) Skinner and Watson - According to constructivists, how is knowledge constructed?
(a) Through external stimuli and reinforcement
(b) Through active participation and personal experience
(c) Through rote-and-drill methods
(d) Through observable behaviors
Answer: (b) Through active participation and personal experience - What characteristic is emphasized by the constructivist approach in Mathematics education?
(a) Memorization of facts and procedures
(b) Deductive reasoning
(c) Active engagement and inquiry
(d) Observable behaviors and responses
Answer: (c) Active engagement and inquiry - In the behaviorist model, what is the main role of the instructor?
(a) To facilitate discussions and guide learners
(b) To engage learners in problem-solving activities
(c) To present information for learners to absorb
(d) To encourage learners to formulate their own ideas
Answer: (c) To present information for learners to absorb - Linear equations are of __________ form.
a) ax2+bx+c = 0
b) ax+by+c = 0
c) x2+y2 = a2
d) x2-y2 = a2
Answer: b
Explanation: Linear equations of two variables are generally denoted by ax+by+c = 0. - How many solutions does a linear equation have?
a) One
b) Two
c) Three
d) Four
Answer: a
Explanation: Let’s understand this by an example:
Suppose we want to find the solution for 9x-3 = 0
9x-3 = 0
9x = 3
Therefore x = 1/3
We can see that this linear equation has only one solution. i.e. x = 1/3
It means that there is only one number which satisfies the given equation. - Which of the following is the correct way to represent the equation 3x=9 in ax+by+c = 0 form?
a) 3x = -0y + 9
b) 3x + 0y = 9
c) 3x + 0y – 9 = 0
d) 3x + 0y = 9
Answer: c
Explanation: In ax + by + c = 0, a, b and c are numbers and a, b≠0 while x and y are variables.
Given equation is 3x=9.
If we want it to represent in the ax+by+c=0 form, we can write 3x + 0y – 9 = 0 where a = 3, b = 0 and c = -9.
advertisement - Find the solution for the linear equation 2.5x=5?
a) x=-2
b) x=5
c) x=3
d) x=2
Answer: d
Explanation: 2.5x=5
We know that equations is not affected by dividing the same non-zero number both sides.
Hence, dividing the equation by 2.5 both sides.
Therefore x=5/2.5
Hence, x = 2 - Calculate the sum of lengths: 21 m 13 cm, 33 m 55 cm and 45 m 6 cm.
(a) 99 m 70 cm
(b) 99 m 74 cm
(c) 100 m 74 cm
(d) 100 m 70 cm
Ans. (b) 99 m 74 cm
Solution:
21 m 13 cm + 33 m 55 cm + 45 m 6 cm
= (21 + 33 + 45) m (13 + 55 + 6) cm
= 99 m 74 cm
Therefore, the sum of given lengths = 99 m 74 cm. - Beena bought 3 kg 760 grams of wool to make a carpet. How much more wool does she need to make the weight 4 kg?
(a) 200 grams
(b) 220 grams
(c) 240 grams
(d) 260 grams
Ans. (c) 240 grams
Solution:
Given the weight of wool = 3 kg 760 grams
Let us convert this weight into grams.
3 kg 760 grams = (3 × 1000 + 760) grams
= (3000 + 760) grams
= 3760 grams
4 kg = (4 × 1000) grams = 4000 grams
Difference = (4000 – 3760) grams = 240 grams
Therefore, 240 grams of more wool is required. - A pile of 10 books is 10 cm high. What is the thickness of each book?
(a) 8 mm
(b) 9 mm
(c) 10 mm
(d) 11 mm
Ans. (c) 10 mm
Solution:
As we know,
1 cm = 10 mm
Given that the height of a pile of 10 books = 10 cm
10 books = 10 cm
= 10 x 10 mm
= 100 mm
1 book = 100/10
= 10 mm
Therefore, the thickness of each book = 10 mm. - A furlong is a unit of length used in horse racing; it equals one-eighth of a mile. To the nearest tenth, how many metres are equal to a furlong if 1.609 km equals a mile?
(a) 200.0 m
(b) 201.0 m
(c) 201.1 m
(d) 202.0 m
Ans. (c) 201.1 m
Solution:
Given,
1.609 km = 1 mile
That means 1609 m = 1 mile
Also, one furlong = one-eighth of a mile
= (1/8) × 1.609 km
= (1/8) × 1609 m
= 201.125
= 201.1 m (approx) - The cost of 1 litre of syrup is Rs. 840.80. Find the cost of 600 ml of the syrup.
(a) Rs. 502.48
(b) Rs. 503.48
(c) Rs. 504.48
(d) Rs. 505.48
Ans. (c) Rs. 504.48
Solution:
Given,
The cost of 1 litre of syrup = Rs. 840.80
As we know,
1 litre = 1000 ml
The cost of 600 ml of the syrup = (600/1000) × Rs. 840.80 = Rs. 504.48 - Equal _____ of the congruent circles subtend equal angles at the centers.
a. Segments
b. Radii
c. Arcs
d. Chords
Answer: d
Explanation: See the figure below:
Let ΔAOB and ΔCOD be two triangles inside the circle.
OA = OC and OB = OD (radii of the circle)
AB = CD (Given)
So, ΔAOB ≅ ΔCOD (SSS congruency)
∴ By CPCT rule, ∠AOB = ∠COD.
Hence, this proves the statement. - If chords AB and CD of congruent circles subtend equal angles at their centres, then:
a. AB = CD
b. AB > CD
c. AB < CD
d. None of the above
Answer: a
Explanation: Take the reference of the figure from above question.
In triangles AOB and COD,
∠AOB = ∠COD (given)
OA = OC and OB = OD (radii of the circle)
So, ΔAOB ≅ ΔCOD (SAS congruency)
∴ AB = CD (By CPCT) - If AB and CD are two chords of a circle intersecting at point E, as per the given figure, then:
a. ∠BEQ > ∠CEQ
b. ∠BEQ = ∠CEQ
c. ∠BEQ < ∠CEQ
d. None of the above
Answer: b
Explanation:
OM = ON (Equal chords are always equidistant from the centre)
OE = OE (Common)
∠OME = ∠ONE (perpendiculars)
So, ΔOEM ≅ ΔOEN (by RHS similarity criterion)
Hence, ∠MEO = ∠NEO (by CPCT rule)
∴ ∠BEQ = ∠CEQ - If a line intersects two concentric circles with centre O at A, B, C and D, then:
a. AB = CD
b. AB > CD
c. AB < CD
d. None of the above
Answer: a
Explanation: See the figure below:
From the above fig., OM ⊥ AD.
Therefore, AM = MD — 1
Also, since OM ⊥ BC, OM bisects BC.
Therefore, BM = MC — 2
From equation 1 and equation 2.
AM – BM = MD – MC
∴ AB = CD - In the below figure, the value of ∠ADC is:
a. 60°
b. 30°
c. 45°
d. 55°
Answer: c
Explanation: ∠AOC = ∠AOB + ∠BOC
So, ∠AOC = 60° + 30°
∴ ∠AOC = 90°
An angle subtended by an arc at the centre of the circle is twice the angle subtended by that arc at any point on the rest part of the circle.
So,
∠ADC = 1/2∠AOC
= 1/2 × 90° = 45° - Find the surface area of the given cuboid.
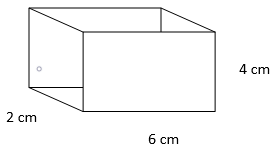
a) 44 cm2
b) 22 cm2
c) 40 cm2
d) 88 cm2
Answer: d
Explanation: Surface area cuboid = 2(lb + bh + lh) = 2(6 × 4 + 4 × 2 + 2 × 6) = 88 cm2. - What is the surface area of the given cube?
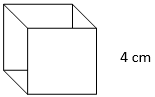
a) 46 cm2
b) 96 cm2
c) 48 cm2
d) 92 cm2
Answer: b
Explanation: Surface area cube = 6 a2 = 6 (42) = 96 cm2. - Find the surface area of the given cylinder.
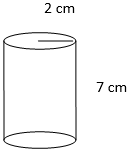
a) 113.14 cm2
b) 113.16 cm2
c) 112.16 cm2
d) 112.14 cm2
Answer: a
Explanation: Curved Surface area of cylinder = 2πrh + 2πr2 = 2πr(r + h) = 2 × 227 × 2(2 + 7)
= 113.14 cm2.
advertisement - A gift in the form of cube has to be wrapped with gift paper whose external measures are 15 cm. Find the area of gift paper needed.
a) 1250 cm2
b) 1354 cm2
c) 1350 cm2
d) 1150 cm2
Answer: c
Explanation: Surface area cube = 6 a2 = 6 (152) = 1350 cm2. - The internal measurement of a cuboidal room 15m × 6m × 4m.The room has to be painted along with the ceiling. If cost of painting is Rs 17 per m2, Find the total cost to be paid.
a) Rs 4916
b) Rs 3916
c) Rs 4686
Answer: d
Explanation: Surface area cuboid = 2(lb + bh + lh)
The floor of the room will not be painted.
∴ Surface area to be painted = 2(lb + bh + lh) – lb
= 2(15 × 6 + 4 × 6 + 4 × 15) – 15 × 6 = 258 m2
Total cost to be paid = 258 × 17 = Rs 4386. - A building has 6 cylindrical pillars whose radius is 2m and height is 12m. Each pillar has to be painted and the cost of painting is Rs 22 per meter sq. Find the cost of painting the curved surface area of the 6 pillars.
a) Rs. 3872
b) Rs. 13232
c) Rs. 7744
d) Rs. 23232
Answer: d
Explanation: Curved Surface area of cylinder = 2πrh + 2πr2 = 2πr(r + h) = 2 × 227 × 2(2 + 12)
= 176 m2
The total cost of painting 1 pillar = 176 × 22 = Rs. 3872.
The total cost of painting 6 pillars = 3872 × 6 = Rs. 23232.










