Mathematics is an integral part of various competitive exams, including the OSSSC (Odisha Subordinate Staff Selection Commission) RI (Revenue Inspector), ARI (Assistant Revenue Inspector), Amin, SFS, and ICDS Supervisor exams. To excel in these exams, candidates need to have a solid understanding of mathematical concepts and problem-solving skills. To help you prepare effectively, we’ve compiled a list of the top 30 Mathematics Multiple Choice Questions (MCQs) commonly encountered in these exams.
Top 30 Mathematics MCQS For OSSSC RI,ARI, Amin, SFS, ICDS Supervisor
- Find the greatest number that will divide 43, 91, and 183 so as to leave the same remainder in each case.
(a) 4
(b) 7
(c) 9
(d) 13
Ans: (a)
Explanation: Required number = H.C.F. of (91 – 43), (183 – 91), and (183 – 43)
= H.C.F. of 48, 92, and 140 = 4. - The H.C.F. of two numbers is 23, and the other two factors of their L.C.M. are 13 and 14. The larger of the two numbers is:
(a) 276
(b) 299
(c) 322
(d) 345
Ans: (c)
Explanation: The numbers are (23 × 13) and (23 × 14).
Larger number = (23 × 14) = 322. - Six bells commence tolling together and toll at intervals of 2, 4, 6, 8, 10, and 12 seconds respectively. In 30 minutes, how many times do they toll together?
(a) 4
(b) 10
(c) 15
(d) 16
Ans: (d)
Explanation: L.C.M. of 2, 4, 6, 8, 10, and 12 is 120 seconds (2 minutes).
In 30 minutes, they will toll together 30/2 + 1 = 16 times. - Let N be the greatest number that will divide 1305, 4665, and 6905, leaving the same remainder in each case. Then the sum of the digits in N is:
(a) 4
(b) 5
(c) 6
(d) 8
Ans: (a)
Explanation: N = H.C.F. of (4665 – 1305), (6905 – 4665), and (6905 – 1305)
= H.C.F. of 3360, 2240, and 5600 = 1120.
Sum of digits in N = (1 + 1 + 2 + 0) = 4. - The greatest number of four digits which is divisible by 15, 25, 40, and 75 is:
(a) 9000
(b) 9400
(c) 9600
(d) 9800
Ans: (c)
Explanation: The greatest number of 4 digits is 9999.
L.C.M. of 15, 25, 40, and 75 is 600.
On dividing 9999 by 600, the remainder is 399.
Required number = (9999 – 399) = 9600. - A person crosses a 600 m long street in 5 minutes. What is his speed in km per hour?
(a) 3.6
(b) 7.2
(c) 8.4
(d) 10
Ans: (b)
Explanation:
- An aeroplane covers a certain distance at a speed of 240 kmph in 5 hours. To cover the same distance in 1 hour, it must travel at a speed of:
(a) 300 kmph
(b) 360 kmph
(c) 600 kmph
(d) 720 kmph
Ans: (d)
Explanation: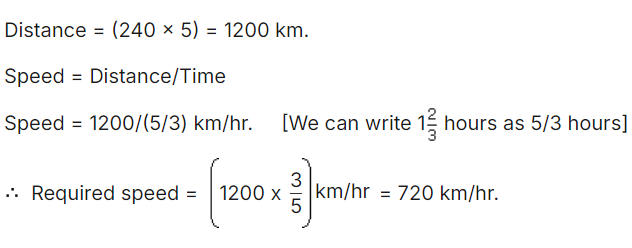
- If a person walks at 14 km/hr instead of 10 km/hr, he would have walked 20 km more. The actual distance travelled by him is:
(a) 50 km
(b) 56 km
(c) 70 km
(d) 80 km
Ans: (a)
Explanation:
- A train can travel 50% faster than a car. Both start from point A at the same time and reach point B, 75 kms away from A, at the same time. On the way, however, the train lost about 12.5 minutes while stopping at the stations. The speed of the car is:
(a) 100 kmph
(b) 110 kmph
(c) 120 kmph
(d) 130 kmph
Ans: (c)
Explanation:
- Excluding stoppages, the speed of a bus is 54 kmph and including stoppages, it is 45 kmph. For how many minutes does the bus stop per hour?
(a) 9
(b) 10
(c) 12
(d) 20
Ans: (b)
Explanation:
- Two ships are sailing in the sea on the two sides of a lighthouse. The angle of elevation of the top of the lighthouse observed from the ships are 30° and 45° respectively. If the lighthouse is 100 m high, the distance between the two ships is:
(a) 173 m
(b) 200 m
(c) 273 m
(d) 300 m
Ans: (c) 273 m
Explanation: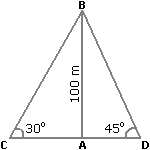
Let AB be the lighthouse and C and D be the positions of the ships.
AB = 100 m, ACB = 30°, ADB = 45°
AC = AB × √3 = 100√3 m
AD = AB = 100 m
CD = AC + AD = 100√3 + 100 = 100(√3 + 1) = 100 × 2.73 = 273 m - A man standing at a point P is watching the top of a tower, which makes an angle of elevation of 30° with the man’s eye. The man walks some distance towards the tower to watch its top, and the angle of elevation becomes 60°. What is the distance between the base of the tower and the point P?
(a) 43 units
(b) 8 units
(c) 12 units
(d) Data inadequate
(e) None of these
Ans: (d) Data inadequate
Explanation: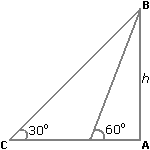
To solve this problem, we need additional information such as the height of the tower or the distance walked by the man. Therefore, the data provided is inadequate to determine the distance. - The angle of elevation of a ladder leaning against a wall is 60° and the foot of the ladder is 4.6 m away from the wall. The length of the ladder is:
(a) 2.3 m
(b) 4.6 m
(c) 7.8 m
(d) 9.2 m
Ans: (d) 9.2 m
Explanation: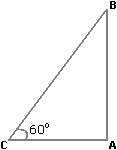
Let AB be the wall and BC be the ladder.
ACB = 60°, AC = 4.6 m
cos 60° = AC/BC = 1/2
BC = 2 × AC = 2 × 4.6 = 9.2 m - An observer 1.6 m tall is 20 m away from a tower. The angle of elevation from his eye to the top of the tower is 30°. The height of the tower is:
(a) 21.6 m
(b) 23.2 m
(c) 24.72 m
(d) None of these
Ans: (a) 21.6 m
Explanation: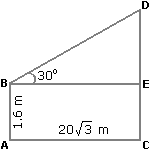
Let the height of the tower be h meters.
The height difference is given by tan 30° = (h – 1.6) / 20
√3/3 = (h – 1.6) / 20
h – 1.6 = 20 × √3/3
h = 20 × 1.73 / 3 + 1.6 = 11.54 + 1.6 = 21.6 m - From a point P on a level ground, the angle of elevation of the top of a tower is 30°. If the tower is 100 m high, the distance of point P from the foot of the tower is:
(a) 149 m
(b) 156 m
(c) 173 m
(d) 200 m
Ans: (c) 173 m
Explanation: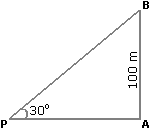
Let AB be the tower and P be the point on the ground.
tan 30° = AB / AP = 1 / √3
AP = AB × √3 = 100 × 1.73 = 173 m - A sum of money at simple interest amounts to Rs. 815 in 3 years and to Rs. 854 in 4 years. The sum is:
(a) Rs. 650
(b) Rs. 690
(c) Rs. 698
(d) Rs. 700
Ans: (c) Rs. 698
Explanation: S.I. for 1 year = Rs. (854 – 815) = Rs. 39.
S.I. for 3 years = Rs.(39 x 3) = Rs. 117.
Principal = Rs. (815 – 117) = Rs. 698. - Mr. Thomas invested an amount of Rs. 13,900 divided in two different schemes A and B at the simple interest rate of 14% p.a. and 11% p.a. respectively. If the total amount of simple interest earned in 2 years is Rs. 3508, what was the amount invested in Scheme B?
(a) Rs. 6400
(b) Rs. 6500
(c) Rs. 7200
(d) Rs. 7500
(e) None of these
Ans: (a) Rs. 6400
Explanation:
- A sum fetched a total simple interest of Rs. 4016.25 at the rate of 9 p.c.p.a. in 5 years. What is the sum?
(a) Rs. 4462.50
(b) Rs. 8032.50
(c) Rs. 8900
(d) Rs. 8925
(e) None of these
Ans: (d) Rs. 8925
Explanation: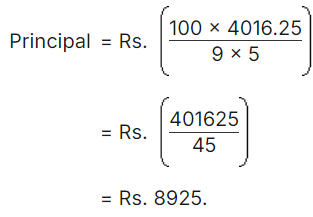
- How much time will it take for an amount of Rs. 450 to yield Rs. 81 as interest at 4.5% per annum of simple interest?
(a) 3.5 years
(b) 4 years
(c) 4.5 years
(d) 5 years
Ans: (b) 4 years
Explanation: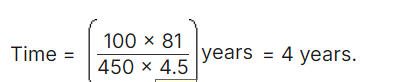
- Reena took a loan of Rs. 1200 with simple interest for as many years as the rate of interest. If she paid Rs. 432 as interest at the end of the loan period, what was the rate of interest?
(a) 3.6
(b) 6
(c) 18
(d) Cannot be determined
(e) None of these
Ans: (b) 6
Explanation: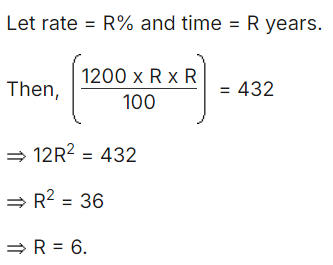
- A man has Rs.480 in the denominations of one-rupee notes, five-rupee notes, and ten-rupee notes. The number of notes of each denomination is equal. What is the total number of notes that he has?
(A) 45
(B) 60
(C) 75
(D) 90
Answer: D
Explanation: Let number of notes of each denomination be x.
Then x + 5x + 10x = 480
16x = 480
x = 30.
Hence, total number of notes = 3x = 90. - There are two examination rooms A and B. If 10 students are sent from A to B, then the number of students in each room is the same. If 20 candidates are sent from B to A, then the number of students in A is double the number of students in B. The number of students in room A is:
(A) 20
(B) 80
(C) 100
(D) 200
Answer: C
Explanation: Let the number of students in rooms A and B be x and y respectively.
Then, x – 10 = y + 10 = x – y = 20 …. (I)
and x + 20 = 2(y – 20) = x – 2y = -60 …. (ii)
Solving (i) and (ii) we get: x = 100 , y = 80.
The required answer A = 100. - The price of 10 chairs is equal to that of 4 tables. The price of 15 chairs and 2 tables together is Rs. 4000. The total price of 12 chairs and 3 tables is:
(A) Rs. 3500
(B) Rs. 3750
(C) Rs. 3840
(D) Rs. 3900
Answer: D
Explanation: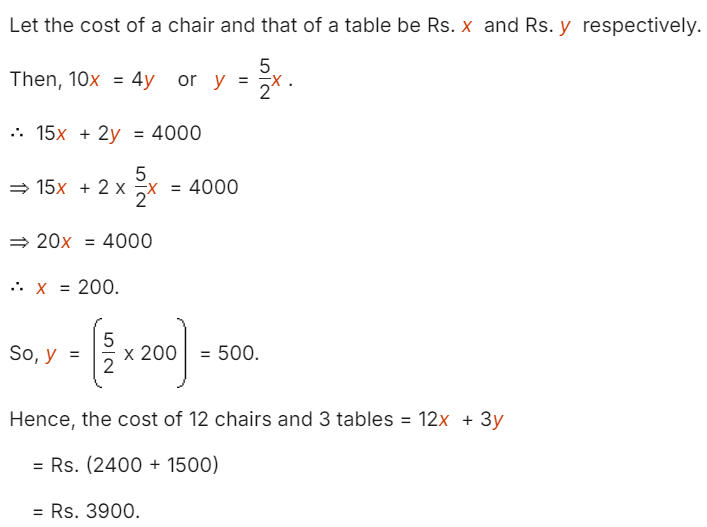
- If a-b=3 and a2-b =29, find the value of(A) 10
(B) 12
(C) 15
(D) 18
Answer: A
Explanation: 2ab = (a2 + b2) – (a – b)2
= 29 – 9 = 20
ab = 10. - The price of 2 sarees and 4 shirts is Rs. 1600. With the same money, one can buy 1 saree and 6 shirts. If one wants to buy 12 shirts, how much shall he have to pay?
(A) Rs. 1200
(B) Rs. 2400
(C) Rs. 4800
(D) Cannot be determined
(E) None of these
Answer: B
Explanation: Let the price of a saree and a shirt be Rs. x and Rs. y respectively.
Then, 2x + 4y = 1600 …. (i)
and x + 6y = 1600 …. (ii)
Solving (i) and (ii) we get x = 400, y = 200.
Cost of 12 shirts = Rs. (12 x 200) = Rs. 2400. - 3, 5, 11, 14, 17, 21
(A) 21
(B) 17
(C) 14
(D) 3
Answer: C
Explanation: Each of the numbers except 14 is an odd number. The number ’14’ is the only even number. - 8, 27, 64, 100, 125, 216, 343
(A) 27
(B) 100
(C) 125
(D) 343
Answer: B
Explanation: The pattern is 23, 33, 43, 53, 63, 73. But, 100 is not a perfect cube. - 10, 25, 45, 54, 60, 75, 80
(A) 10
(B) 45
(C) 54
(D) 75
Answer: C
Explanation: Each of the numbers except 54 is a multiple of 5. - 396, 462, 572, 427, 671, 264
(A) 396
(B) 427
(C) 671
(D) 264
Answer: B
Explanation: In each number except 427, the middle digit is the sum of the other two digits. - 6, 9, 15, 21, 24, 28, 30
(A) 28
(B) 21
(C) 24
(D) 30
Answer: A
Explanation: Each of the numbers except 28 is a multiple of 3.





