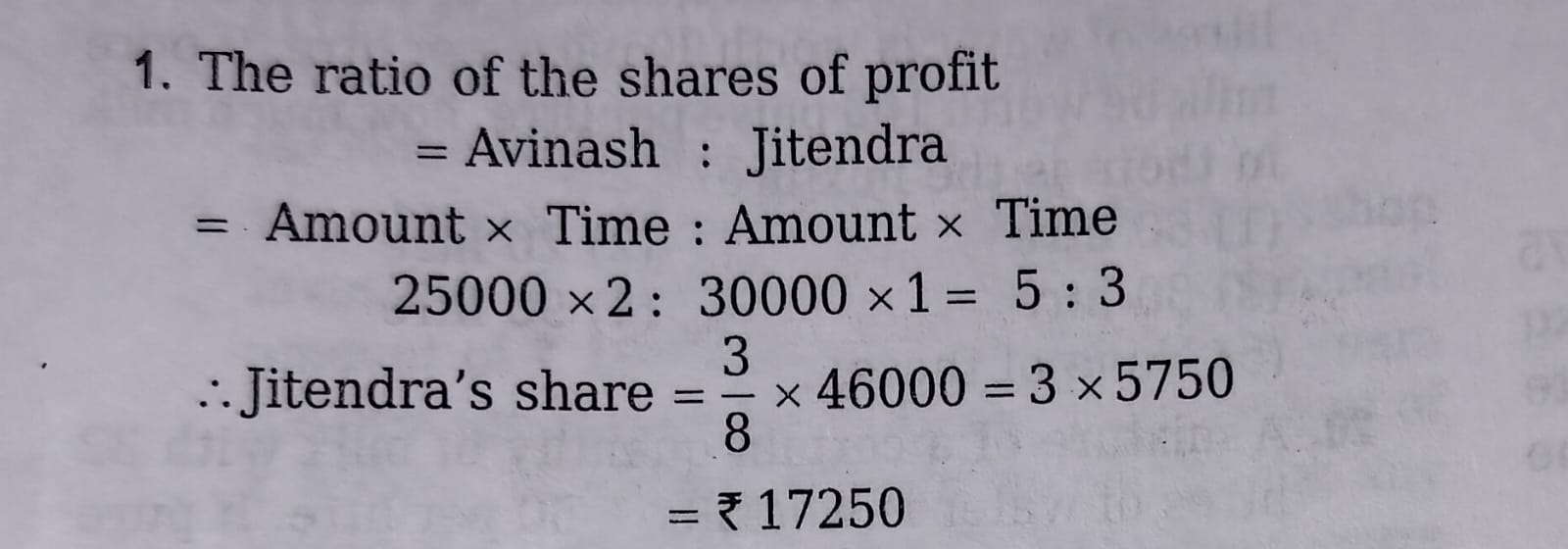Mathematics is an integral part of various competitive exams, including the OSSSC (Odisha Subordinate Staff Selection Commission) RI (Revenue Inspector), ARI (Assistant Revenue Inspector), Amin, SFS, and ICDS Supervisor exams. To excel in these exams, candidates need to have a solid understanding of mathematical concepts and problem-solving skills. To help you prepare effectively, we’ve compiled a list of the top 30 Mathematics Multiple Choice Questions (MCQs) commonly encountered in these exams.
Top 30 Mathematics MCQS For OSSSC RI,ARI, Amin, SFS, ICDS Supervisor
- Avinash invested an amount of₹ 25000 and started a business. Jitendra joined him after one year with an amount of₹ 30000. After two years from starting the business they earned the profit of 46000. What will be Jitendra’s share in the profit?
(a) ₹14000
(b) ₹12000
(c)₹ 766.67
(d) None of these
Ans: (d) None of these - Mr. Nilesh Agrawal opened a workshop investing 40000. He invested additional amount of 10000 every year. After two years his brother Suresh joined him with an amount of 85000. Thereafter Suresh did not invest any additional amount. On completion of four years from the opening of workshop they earned an amount of 195000. What will be Nilesh’s share in the earning?
(a) ₹ 85000
(b) ₹110000
(c) ₹135000
(c) ₹95000
Ans: (b) ₹110000
- What is the average of the first 50 natural numbers?
(a) 24.5
(b) 25.5
(c) 26.5
(d) 27.5
Ans: (b) 25.5
Solution: Sum of the first 50 natural numbers = 50 * 51 / 2 = 1275. Average = 1275 / 50 = 25.5. - The average of 20 numbers is zero. Of them, at the most, how many may be greater than zero?
(a) 0
(b) 1
(c) 10
(d) 19
Ans: (d) 19
Solution: The sum of all 20 numbers is zero. To keep the average zero, the sum of positive numbers must be equal to the sum of negative numbers. At most 19 numbers can be positive if one number is large enough negative to balance them. - If the price of a book is increased by 20%, by what percentage should the sales price be decreased to bring it back to the original price?
(a) 16%
(b) 20%
(c) 25%
(d) 10%
Ans: (a) 16%
Solution: Let the original price be 100. Increased price = 120. To bring it back to 100, the decrease should be
20/120×100=16.67% - A number is increased by 20% and then decreased by 20%. What is the net change in the number?
(a) 0%
(b) 4% increase
(c) 4% decrease
(d) 2% decrease
Ans: (c) 4% decrease
Solution: Let the number be 100. After a 20% increase, it becomes 120. After a 20% decrease, it becomes 120 – 24 = 96. Net change = 100 – 96 = 4% decrease. - What is the remainder when 7^103 is divided by 24?
(a) 1
(b) 7
(c) 19
(d) 23
Ans: (b) 7
Solution: Using Fermat’s Little Theorem,
7^3≡1, mod 24mod24. Therefore,
7 ^103 ≡7, mod24. - Find the largest 4-digit number which is divisible by 12, 15, and 18.
(a) 9900
(b) 9960
(c) 9990
(d) 9980
Ans: (b) 9960
Solution: LCM of 12, 15, and 18 is 180. Largest 4-digit number is 9999.
9999÷180=55.55. Nearest integer is 55.
55×180=9900. - A and B can complete a work in 15 and 20 days respectively. They work together for 4 days, then B leaves. In how many days will A finish the remaining work?
(a) 5
(b) 6
(c) 7
(d) 8
Ans: (d) 8
Solution: Work done by A and B in 4 days = (1/15+1/20)×4=7/15
Remaining work = 1−7/15=8/15
A can finish this in (8/15)/(1/15)=8 days. - Three workers A, B, and C can complete a work in 8, 10, and 12 days respectively. How many days will they take to complete the work together?
(a) 2
(b) 3.24
(c) 4.24
(d) 5
Ans: (b) 3.24
Solution: Work done per day by A, B, and C together =
1/8+1/10+1/12=37/120.
Total time taken = 120/37≈3.24=3.24 days. - Average Marks of Students
Student Marks A 80 B 70 C 90 D 85 What is the average marks of the students from the following table?
(a) 80
(b) 81
(c) 82
(d) 81.25Ans: (d) 81.25
Solution: Add up the marks and divide by the number of students: 80+70+90+854=3254=81.25\frac{80 + 70 + 90 + 85}/{4} = \frac{325}/{4} = 81.25
- If another student E is added to the list, making the new average of the marks equal to 81, what is the mark obtained by E?
- (a) 75
(b) 78
(c) 79
(d) 82
Ans: (b) 78
Solution: Current average = 80+70+90+854=3254=81.25\frac{80 + 70 + 90 + 85}{4} = \frac{325}{4} = 81.25. Let the mark obtained by E be x. New average = 81, thus 325+x5=81⇒325+x=405⇒x=78\frac{325 + x}/{5} = 81 \⇒325 + x = 405 \⇒x = .
- (a) 75
- If student A’s mark increases by 10% and student D’s mark decreases by 10%, what will be the new average mark of the students?
- (a) 81
(b) 81.1
(c) 82
(d) 82.5
Ans: (b) 81.1
Solution: New mark of A = 80 + 0.180 = 88, new mark of D = 85 – 0.185 = 76.5. New sum = 88 + 70 + 90 + 76.5 = 324.5. New average = 324.54=81.125≈81.5\frac{324.5}{4} = 81.125
- (a) 81
- If the marks of student C decrease by 15% and those of student B increase by 20%, what will be the new average mark of the students?
- (a) 79
(b)
(c) 81.75
(d) 82.25
Ans: (b)
Solution: New mark of C = 90 – 0.1590 = 76.5, new mark of B = 70 + 0.270 = 84. New sum = 80 + 84 + 76.5 + 85 = 325.5. New average = 325.54=81.375≈80.5\frac{325.5}{4} = 81.375 \
- (a) 79
- If a student F with a mark equal to the average mark of the original four students is added to the list, what will be the new average mark?
- (a) 80
(b) 81
(c) 82
(d) 83
Ans: (b) 81
Solution: Average mark of the original four students = 81. Mark of student F = 81. New sum = 80 + 70 + 90 + 85 + 81 = 406. New average = 4065=81.2≈81\frac{406}/{5} = 81.2 .
- (a) 80
- A car travels 250 miles in 5 hours. How many miles will it travel in 7 hours?
(a) 350
(b) 400
(c) 450
(d) 500
Ans: (b) 400
Solution: Multiply the distance traveled in 5 hours by 7/5. - What is the value of 3^4 × 3^2?
(a) 3^6
(b) 3^8
(c) 3^10
(d) 3^12
Ans: (a) 3^6
Solution: Use the property of exponents that states a^m × a^n = a^(m+n). - A bakery sells 250 loaves of bread at Rs. 20 each. If the cost price is Rs. 15 per loaf, what is the profit percentage?
(a) 25%
(b) 33.33%
(c) 40%
(d) 50%
Ans: (b) 33.33%
Solution: Calculate the profit and divide by the cost price, then multiply by 100. - What is the value of x in the equation 3x – 7 = 2x + 5?
(a) 4
(b) 5
(c) 6
(d) 8
Ans: (c) 6
Solution: Add 7 to both sides, then subtract 2x from both sides. - A car travels from city A to city B at an average speed of 60 km/h and returns at an average speed of 40 km/h. What is the average speed for the entire journey?
(a) 48 km/h
(b) 50 km/h
(c) 52 km/h
(d) 55 km/h
Ans: (a) 48 km/h
Solution: Use the formula for average speed: (2xy)/(x+y)=(2*60*40)/(40+60)= 48km/h - A shop sells 200 units of a product at Rs. 50 each. If the cost price is Rs. 30 per unit, what is the profit percentage?
(a) 40%
(b) 50%
(c) 60%
(d) 66.67%
Ans: (d) 66.67%
Solution: Calculate the profit and divide by the cost price, then multiply by 100. - A bicycle costs Rs. 1200. If a 15% discount is offered, what is the new price?
(a) Rs. 960
(b) Rs. 1020
(c) Rs. 1020
(d) Rs. 1050
Ans: (b) Rs. 1020
Solution: Calculate 15% of the original price and subtract it from the original price. 1200-1200*15/100=1020 - A water tank can hold 5000 liters of water. If 2000 liters are already filled, what percentage is filled?
(a) 40%
(b) 45%
(c) 50%
(d) 55%
Ans: (a) 40%
Solution: Divide the amount filled by the total capacity and multiply by 100. 2000/5000*100=40% - A person invests Rs. 2000 at an interest rate of 12% per annum. How much will he earn in 3 years?
(a) Rs. 600
(b) Rs. 720
(c) Rs. 840
(d) Rs. 960
Ans: (c) Rs. 840
Solution: Calculate the interest for 3 years using the formula: (Principal x Rate x Time)/100 - A shop sells 200 units of a product at Rs. 100 each. If the cost price is Rs. 80 per unit, what is the profit percentage?
(a) 20%
(b) 25%
(c) 30%
(d) 35%
Ans: (b) 25%
Solution: Calculate the profit and divide by the cost price, then multiply by 100. - A bag contains 50 P, 25 P, and 10 P coins in the ratio 5:9:4, amounting to Rs. 206. Find the number of coins of each type respectively.
(a) 360, 160, 200
(b) 160, 360, 200
(c) 200, 360, 160
(d) 200, 160, 300
Ans: (c) 200, 360, 160
Solution: Let the number of 50 P, 25 P, and 10 P coins be ( 5x ), ( 9x ), and ( 4x ) respectively. The total value is ( 50 \times 5x + 25 \times 9x + 10 \times 4x = 20600 ) paise. Solving for ( x ), we find ( x = 40 ). Therefore, the number of coins is 200, 360, and 160. - Two numbers are respectively 20% and 50% more than a third number. What is the ratio of the two numbers?
(a) 2:5
(b) 3:5
(c) 4:5
(d) 5:4
Ans: (c) 4:5
Solution: Let the third number be ( x ). The first number is ( 1.2x ) and the second number is ( 1.5x ). The ratio is ( \frac{1.2x}{1.5x} = \frac{4}{5} ). - If the cost price of 15 articles is equal to the selling price of 12 articles, find the profit percentage.
(a) 20%
(b) 25%
(c) 30%
(d) 40%
Ans: (b) 25%
Solution: Let the cost price of one article be ( x ). Therefore, the cost price of 15 articles is ( 15x ) and the selling price of 12 articles is ( 15x ). Hence, the selling price of one article is ( \frac{15x}{12} = 1.25x ). Profit percentage = ( \frac{1.25x – x}{x} \times 100 = 25% ). - A TV was originally priced at $800. It is now being sold at a discount of 20%. What is the discounted price?
(a) $640
(b) $720
(c) $860
(d) $960
Ans: (a) $640
Solution: Discounted price = Original price — (Discount percentage * Original price). Discounted price = $800 — (20% * $800) = $800 — $160 = $640. - The average of five numbers is 32. If one of the numbers is 45, what is the average of the remaining numbers?
(a) 30
(b) 34
(c) 35
(d) 36
Ans: (c) 35 Solution: Sum of the five numbers = 32 * 5 = 160. Sum of the remaining four numbers = 160–45 = 115. Average of the remaining numbers = 115 / 4 = 28.75.