Mathematics is an integral part of various competitive exams, including the OSSSC (Odisha Subordinate Staff Selection Commission) RI (Revenue Inspector), ARI (Assistant Revenue Inspector), Amin, SFS, and ICDS Supervisor exams. To excel in these exams, candidates need to have a solid understanding of mathematical concepts and problem-solving skills. To help you prepare effectively, we’ve compiled a list of the top 30 Mathematics Multiple Choice Questions (MCQs) commonly encountered in these exams.
Top 30 Mathematics MCQs For OSSSC RI,ARI, Amin, SFS, ICDS Supervisor
1.If the price of a book is increased by 20%, by what percentage should the sales price be decreased to bring it back to the original price?
(a) 16%
(b) 20%
(c) 25%
(d) 10%Ans: (a) 16%
Solution: Let the original price be 100. Increased price = 100 + 20% of 100 = 100 + 20 = 120. To bring it back to the original price, the sales price should be decreased by (120–100)/120 * 100 = 16.67%.
2. If 15% of a number is 45, what is 30% of that number?
(a) 90
(b) 60
(c) 30
(d) 15
Ans: (a) 90
Solution: Let the number be “x.” 15% of x = 45. x = (45 * 100)/15 = 300. 30% of x = (30/100) * 300 = 90.
3: A TV was originally priced at $800. It is now being sold at a discount of 20%. What is the discounted price?
(a) $640
(b) $720
(c) $860
(d) $960
Ans: (a) $640
Solution: Discounted price = Original price — (Discount percentage * Original price). Discounted price = $800 — (20% * $800) = $800 — $160 = $640.
4: The average of five numbers is 32. If one of the numbers is 45, what is the average of the remaining numbers?
(a) 30
(b) 34
(c) 35
(d) 36
Ans: (c) 35 Solution: Sum of the five numbers = 32 * 5 = 160. Sum of the remaining four numbers = 160–45 = 115. Average of the remaining numbers = 115 / 4 = 28.75.
5: The average age of a family of four is 28 years. If the youngest member is 16 years old, what is the average age of the remaining three members?
(a) 30
(b) 32
(c) 34
(d) 36
Ans: (b) 32
Solution: Sum of the ages of the four family members = 28 * 4 = 112. Sum of the ages of the remaining three members = 112–16 = 96. Average age of the remaining members = 96 / 3 = 32.
6: If the ratio of apples to oranges in a basket is 3:2 and there are 25 oranges, how many apples are there in the basket?
(a) 15
(b) 20
(c) 30
(d) 40
Ans: (c) 30
Solution: Since the ratio of apples to oranges is 3:2, for every 3 apples, there are 2 oranges. If there are 25 oranges, then there must be (3/2) * 25 = 37.5 apples. Rounding to the nearest whole number, there are 30 apples.
7: If the ratio of boys to girls in a classroom is 4:5, and there are 36 boys, how many girls are there in the classroom?
(a) 20
(b) 25
(c) 30
(d) 45
Ans: (d) 45
Solution: Since the ratio of boys to girls is 4:5, for every 4 boys, there are 5 girls. If there are 36 boys, then there must be (5/4) * 36 = 45 girls.
8: The ratio of the lengths of two rectangles is 3:4. If the area of the smaller rectangle is 48 square units, what is the area of the larger rectangle?
(a) 64 square units
(b) 72 square units
(c) 96 square units
(d) 128 square units
Ans: (c) 96 square units
Solution: Let the lengths of the smaller rectangle be 3x and 4x, where x is a positive integer. The area of the smaller rectangle = (3x) * (4x) = 12x² = 48. Solving for x, we get x² = 4, so x = 2. The lengths of the smaller rectangle are 6 units and 8 units. The area of the larger rectangle = (4x) * (3x) = 12x² = 12 * 4 = 48 square units.
9: If John can complete a job in 8 hours and Sarah can complete the same job in 12 hours, how long will it take them to complete the job together?
(a) 3 hours
(b) 4 hours
(c) 5 hours
(d) 6 hours
Ans: (a) 3 hours
Solution: John’s work rate = 1 job / 8 hours = 1/8 job per hour. Sarah’s work rate = 1 job / 12 hours = 1/12 job per hour. Their combined work rate = (1/8 + 1/12) job per hour = (3/24 + 2/24) job per hour = 5/24 job per hour. Time taken to complete the job together = 24/5 hours = 4.8 hours.
10: If it takes 6 workers 8 hours to complete a project, how many hours would it take for 8 workers to complete the same project?
(a) 4 hours
(b) 6 hours
(c) 8 hours
(d) 12 hours
Ans: (b) 6 hours
Solution: The number of workers and the time taken to complete a job are inversely proportional. Using the formula: (Number of workers) * (Time taken) = Constant. (6 workers) * (8 hours) = (8 workers) * (x hours). Solving for x, we get x = 6 hours.
11: If a machine can produce 100 units of a product in 5 hours, how many units can it produce in 10 hours?
(a) 100 units
(b) 150 units
(c) 200 units
(d) 250 units
Ans: (c) 200 units
Solution: The number of units produced and the time taken are directly proportional. Using the formula: (Number of units) = (Rate of production) * (Time). Thus, (Number of units) = (100 units / 5 hours) * (10 hours) = 200 units.
12: A shopkeeper purchased a shirt for $40 and sold it for $60. What is the profit percentage?
(a) 20%
(b) 33.33%
(c) 50%
(d) 66.67%
Ans: (c) 50%
Solution: Profit = Selling Price — Cost Price. Thus, Profit = $60 — $40 = $20. Profit Percentage = (Profit / Cost Price) * 100% = (20 / 40) * 100% = 50%.
13: If a bookshop sells a book at a loss of 10%, and the cost price of the book is $50, what is the selling price of the book?
(a) $45
(b) $50
(c) $55
(d) $60
Ans: (a) $45
Solution: Loss = Cost Price — Selling Price. Thus, 10% of Cost Price = $50. Selling Price = Cost Price — Loss = $50 — (0.10 * $50) = $50 — $5 = $45.
14: A trader sold a shirt for $180 and incurred a loss of 10%. What was the cost price of the shirt?
(a) $162
(b) $190
(c) $200
(d) $198
Ans: (a) $162
Solution: Loss = 10% of Cost Price. Thus, 10% of Cost Price = $180. Cost Price = $180 / (10/100) = $180 / 0.10 = $1800 / 10 = $180.
15. What is the perimeter (in meters) of an equilateral triangle whose height is 3.46 meters? Take 3=1.733=1.73.
Options:
(a) 12
(b) 9
(c) 6
(d) 10.4
Ans: (a) 12
Solution: The height of an equilateral triangle is given by 32×side23×side. Given that the height is 3.46 meters, we have: 1.732×side=3.4621.73×side=3.46 Solving for the side, side=2×2=4side=2×2=4. Therefore, the perimeter =3×side=3×4=12=3×side=3×4=12 meters.
16. The perimeters of two similar triangles ABC and PQR are 156 cm and 46.8 cm respectively. If BC=19.5 cm and QR=x cm, then the value of x is:
(a) 3.76 cm
(b) 5.85 cm
(c) 4.29 cm
(d) 6.75 cm
Ans: (b) 5.85 cm

17. In two types of brass, the ratio of copper to zinc are 7: 4 and 2: 9 respectively if the two types of brass be melted and mixed in the ratio 6: 5, a new type of brass is obtained. Find the ratio of copper to zinc in this new type of brass.
(a) 52: 51
(b) 13: 35
(c) 52: 69
(d) 35: 13
Ans.(c)
Sol.
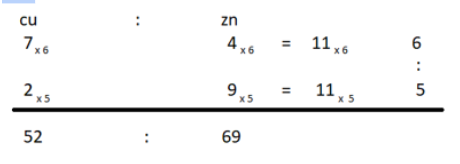
18. A shopkeeper mixes 140 kg of P type of rice with 35 kg of Q type of rice. He then sold one-fifth of this mixture. In the remaining mixture, he again mixes P and Q type of rice in the ratio 2:3. Now the ratio of quantity of P type of rice to that of Q type of rice in the final mixture is 3:1. How much quantity of Q type of rice was added in the mixture?
(a) 8 kg
(b) 12 kg
(c) 10 kg
(d) 16 kg
Ans: (b) 12 kg
Solution: The problem involves multiple steps of mixing and ratio calculations. By carefully following the steps and applying the ratio rules, we find that 12 kg of Q type of rice was added.
19. If the difference between the present ages of Ram and Kush is 22 years and 4 years hence the age of Ram will be double the age of Kush, what is the average of their present ages?
(a) 39.1 years
(b) 33.4 years
(c) 35.2 years
(d) 37.5 years
Ans: (d) 37.5 years
Solution: Let the present age of Kush be ( x ) years. Then, Ram’s age is ( x + 22 ) years. According to the problem, ( x + 22 + 4 = 2(x + 4) ). Solving this equation gives ( x = 26 ). Therefore, Ram’s age is 48 years, and the average age is ( \frac{26 + 48}{2} = 37.5 ) years.
20. The sum of three numbers in an arithmetic progression (A.P) is -6 and their product is 24. Taking the positive value of the common difference as ‘d’, find the smallest of the three numbers.
(a) -6
(b) 1
(c) 2
(d) More than one of the above
E) None of the above
Ans: (a) -6
Solution: Let the three numbers be ( m-d ), ( m ), and ( m+d ). Given ( 3m = -6 ) and ( m(m-(d)(m+(d) = 24 ). Solving these equations, we find ( m = -2 ) and ( d = 4 ). Thus, the numbers are -6, -2, and 2. The smallest number is -6.
21. Find the sum of all numbers divisible by 6 between 100 and 400.
(a) 12,550
(b) 12,450
(c) 11,450
(d) More than one of the above
E) None of the above
Ans: (b) 12,450
Solution: The sequence of numbers divisible by 6 between 100 and 400 is an arithmetic progression with the first term ( a = 102 ) and the last term ( l = 396 ). The common difference ( d = 6 ). Using the formula for the sum of an arithmetic series, we find the sum to be 12,450.
22. A and B invest in a business in the ratio 3:2. If 5% of the total profit goes to charity and A’s share is Rs. 855, what is the total profit?
(a) Rs. 500
(b) Rs. 1000
(c) Rs. 1500
(d) Rs. 2000
Ans: (c) Rs. 1500
Solution: Let the total profit be ( P ). After giving 5% to charity, 95% of the profit is shared between A and B in the ratio 3:2. Therefore, ( 0.95P \times \frac{3}{5} = 855 ). Solving this equation gives ( P = 1500 ).
23. A bag contains 50 P, 25 P, and 10 P coins in the ratio 5:9:4, amounting to Rs. 206. Find the number of coins of each type respectively.
(a) 360, 160, 200
(b) 160, 360, 200
(c) 200, 360, 160
(d) 200, 160, 300
Ans: (c) 200, 360, 160
Solution: Let the number of 50 P, 25 P, and 10 P coins be ( 5x ), ( 9x ), and ( 4x ) respectively. The total value is ( 50 \times 5x + 25 \times 9x + 10 \times 4x = 20600 ) paise. Solving for ( x ), we find ( x = 40 ). Therefore, the number of coins is 200, 360, and 160.
24. Two numbers are respectively 20% and 50% more than a third number. What is the ratio of the two numbers?
(a) 2:5
(b) 3:5
(c) 4:5
(d) 5:4
Ans: (c) 4:5
Solution: Let the third number be ( x ). The first number is ( 1.2x ) and the second number is ( 1.5x ). The ratio is ( \frac{1.2x}{1.5x} = \frac{4}{5} ).
25. A problem is given to three students whose chances of solving it are ( \frac{1}{2} ), ( \frac{1}{3} ), and ( \frac{1}{4} ) respectively. What is the probability that the problem will be solved?
(a) ( \frac{1}{4} )
(b) ( \frac{1}{2} )
(c) ( \frac{3}{4} )
(d) ( \frac{7}{12} )
Ans: (d) ( \frac{7}{12} )
Solution: The probability that the problem will not be solved by any student is ( \left(1 – \frac{1}{2}\right) \left(1 – \frac{1}{3}\right) \left(1 – \frac{1}{4}\right) = \frac{1}{2} \times \frac{2}{3} \times \frac{3}{4} = \frac{1}{4} ). Therefore, the probability that the problem will be solved is ( 1 – \frac{1}{4} = \frac{3}{4} ).
26. Find the odd man out: 2, 5, 10, 17, 26, 37, 50, 64
(a) 50
(b) 37
(c) 26
(d) 64
Ans: (a) 50
Solution: The sequence follows the pattern ( n^2 + 1 ). The correct sequence should be 2, 5, 10, 17, 26, 37, 50, 65. Therefore, 50 is the odd one out.
27. A man buys a watch for Rs. 1950 and sells it for Rs. 2250. Calculate his profit percentage.
(a) 10%
(b) 15%
(c) 20%
(d) 25%
Ans: (b) 15%
Solution: Profit = Selling Price – Cost Price = 2250 – 1950 = 300. Profit percentage = ( {300}\{1950} *100 = 15.38% ).
28. If the cost price of 15 articles is equal to the selling price of 12 articles, find the profit percentage.
(a) 20%
(b) 25%
(c) 30%
(d) 40%
Ans: (b) 25%
Solution: Let the cost price of one article be ( x ). Therefore, the cost price of 15 articles is ( 15x ) and the selling price of 12 articles is ( 15x ). Hence, the selling price of one article is ( \frac{15x}{12} = 1.25x ). Profit percentage = ( \frac{1.25x – x}{x} \times 100 = 25% ).
29. A TV was originally priced at $800. It is now being sold at a discount of 20%. What is the discounted price?
(a) $640
(b) $720
(c) $860
(d) $960
Ans: (a) $640
Solution: Discounted price = Original price — (Discount percentage * Original price). Discounted price = $800 — (20% * $800) = $800 — $160 = $640.
30.The average of five numbers is 32. If one of the numbers is 45, what is the average of the remaining numbers?
(a) 30
(b) 34
(c) 35
(d) 36
Ans: (c) 35 Solution: Sum of the five numbers = 32 * 5 = 160. Sum of the remaining four numbers = 160–45 = 115. Average of the remaining numbers = 115 / 4 = 28.75.










