Mathematics is an integral part of various competitive exams, including the OSSSC (Odisha Subordinate Staff Selection Commission) RI (Revenue Inspector), ARI (Assistant Revenue Inspector), Amin, SFS, and ICDS Supervisor exams. To excel in these exams, candidates need to have a solid understanding of mathematical concepts and problem-solving skills. To help you prepare effectively, we’ve compiled a list of the top 30 Mathematics Multiple Choice Questions (MCQs) commonly encountered in these exams.
Top 30 Mathematics MCQS For OSSSC RI,ARI, Amin, SFS, ICDS Supervisor
- A right triangle with sides 3 cm, 4 cm, and 5 cm is rotated along the side of 3 cm to form a cone. The volume of the cone so formed is:
(a) 12 cm³
(b) 15 cm³
(c) 16 cm³
(d) 20 cm³
Ans: (a) 12 cm³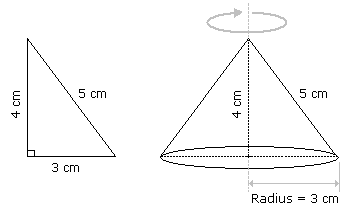
Explanation: Clearly, we have r = 3 cm and h = 4 cm.
Volume = 1/3 πr2h =[1/3 x π x 32 x 4] cm3= 12 πcm3. - In a shower, 5 cm of rain falls. The volume of water that falls on 1.5 hectares of ground is:
(a) 75 cu. m
(b) 750 cu. m
(c) 7500 cu. m
(d) 75000 cu. m
Ans: (b) 750 cu. m
Explanation: 1 hectare = 10,000 m2
So, Area = (1.5 x 10000) m2 = 15000 m2.
Depth = 5m/100= 1/10m Volume = (Area x Depth) =[15000 x1/20]m3 = 750 m3. - A hall is 15 m long and 12 m broad. If the sum of the areas of the floor and the ceiling is equal to the sum of the areas of four walls, the volume of the hall is:
(a) 720 m³
(b) 900 m³
(c) 1200 m³
(d) 1800 m³
Ans: (c) 1200 m³
Explanation: 2(15 + 12) x h = 2(15 x 12)
= h = 180/24 m = 20/3m
Volume =[ 15 x 12 x20/3]m3= 1200 m3 - 66 cubic centimeters of silver is drawn into a wire 1 mm in diameter. The length of the wire in meters will be:
(a) 84 m
(b) 90 m
(c) 168 m
(d) 336 m
Ans: (a) 84 m
Explanation: Let the length of the wire be h.
Radius = 1/2 mm= 1/20cm then
22/7 x 1/20 x1/20 x h = 66
h= [66x20x20x7/22]= 8400 cm = 84 m. - A hollow iron pipe is 21 cm long, and its external diameter is 8 cm. If the thickness of the pipe is 1 cm and iron weighs 8 g/cm³, then the weight of the pipe is:
(a) 3.6 kg
(b) 3.696 kg
(c) 36 kg
(d) 36.9 kg
Ans: (b) 3.696 kg
Explanation:
External radius = 4 cm,
Internal radius = 3 cm.
Volume of iron =[ 22/7 x {(4)2-(3)2}x21] cm3
=[ 22/7 x 7 x 1 x 21] cm3
462 cm3.
=Weight of iron = (462 x 8) gm = 3696 gm = 3.696 kg - Which of the following statements is not correct?
(a) log₁₀ 10 = 1
(b) log (2 + 3) = log (2 × 3)
(c) log₁₀ 1 = 0
(d) log (1 + 2 + 3) = log 1 + log 2 + log 3
Ans: (b)
Explanation:
(a) Since logₐ a = 1, log₁₀ 10 = 1 is correct.
(b) log (2 + 3) = log 5, whereas log (2 × 3) = log 6 ≠ log 5. So, (b) is incorrect.
(c) Since logₐ 1 = 0, log₁₀ 1 = 0 is correct.
(d) log (1 + 2 + 3) = log 6, and log 1 + log 2 + log 3 = log (1 × 2 × 3) = log 6 is correct. - If log 2 = 0.3010 and log 3 = 0.4771, the value of log₅ 512 is:
(a) 2.870
(b) 2.967
(c) 3.876
(d) 3.912
Ans: (c)
Explanation:
log₅ 512 = log 512 / log 5
= log 2⁹ / log (10/2)
= 9 log 2 / (log 10 – log 2)
= (9 × 0.3010) / (1 – 0.3010)
= 2.709 / 0.699
= 3.876 - log₄ √8 is equal to:
(a) log₈ √8
(b) 1/8
(c) 1/4
(d) 1/2
Ans: (c)
Explanation:
log₄ √8 = log₄ (8)¹/₂
= (1/2) log₄ 8
= (1/2) log₄ 2³
= (3/2) log₄ 2
= (3/2) × (1/2)
= 3/4
= 0.75 - If log 27 = 1.431, then the value of log 9 is:
(a) 0.934
(b) 0.945
(c) 0.954
(d) 0.958
Ans: (c)
Explanation:
log 27 = 1.431
log (3³) = 1.431
3 log 3 = 1.431
log 3 = 0.477
log 9 = log (3²) = 2 log 3 = 2 × 0.477 = 0.954 - If log (a/b) + log (b/a) = log (a + b), then:
(a) a + b = 1
(b) a – b = 1
(c) a = b
(d) a² – b² = 1
Ans: (a)
Explanation:
log (a/b) + log (b/a) = log (a + b)
log (a + b) = log [(a × b) / (a × b)] = log 1
So, a + b = 1 - The ratio of the number of boys and girls in a college is 7 : 8. If the percentage increase in the number of boys and girls is 20% and 10% respectively, what will be the new ratio?
(a) 8 : 9
(b) 17 : 18
(c) 21 : 22
(d) Cannot be determined
Ans: (c) 21 : 22
Solution: Originally, let the number of boys and girls in the college be 7x and 8x respectively.
Their increased number is (120% of 7x) and (110% of 8x).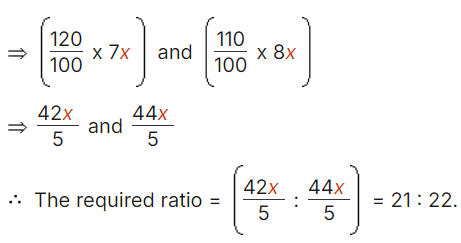
- Salaries of Ravi and Sumit are in the ratio 2 : 3. If the salary of each is increased by Rs. 4000, the new ratio becomes 40 : 57. What is Sumit’s salary?
(a) Rs. 17,000
(b) Rs. 20,000
(c) Rs. 25,500
(d) Rs. 38,000
Ans: (d) Rs. 38,000
Solution: Let the original salaries of Ravi and Sumit be Rs. 2x and Rs. 3x respectively.
Then, 2x+ 4000/3x + 4000 = 40/57
57(2x + 4000) = 40(3x + 4000)
6x = 68,000
3x = 34,000
Sumit’s present salary = (3x + 4000) = Rs.(34000 + 4000) = Rs. 38,000. - 8. If 0.75 : x :: 5 : 8, then x is equal to:
(a) 1.12
(b) 1.2
(c) 1.25
(d) 1.30
Ans: (b) 1.2
Solution: (X x 5) = (0.75 x 8) = x = (6/5)= 1.20 - The sum of three numbers is 98. If the ratio of the first to second is 2 : 3 and that of the second to the third is 5 : 8, then the second number is:
(a) 20
(b) 30
(c) 48
(d) 58
Ans: (b) 30
Solution: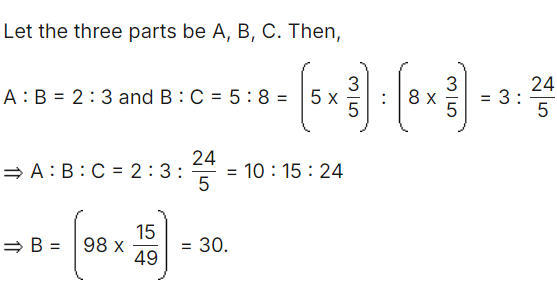
- If Rs. 782 be divided into three parts, proportional to 6 : 8 : 9, then the first part is:
(a) Rs. 182
(b) Rs. 190
(c) Rs. 196
(d) Rs. 204
Ans: (d) Rs. 204
Solution: Given ratio = 1/2: 2/3: 3/4 = 6: 8: 9.
1st part = Rs.(782 x 6/23) = Rs. 204 - If 6th March, 2005 is Monday, what was the day of the week on 6th March, 2004?
(A) Sunday
(B) Saturday
(C) Tuesday
(D) Wednesday
Ans: A
Explanation: The year 2004 is a leap year, so it has 2 odd days. Since February 2004 is not included in the calculation (we’re calculating from March 2004 to March 2005), it has 1 odd day. Therefore, the day on 6th March 2005 is 1 day beyond the day on 6th March 2004. Given that 6th March 2005 is Monday, 6th March 2004 was Sunday. - On what dates of April 2001 did Wednesday fall?
(A) 1st, 8th, 15th, 22nd, 29th
(B) 2nd, 9th, 16th, 23rd, 30th
(C) 3rd, 10th, 17th, 24th
(D) 4th, 11th, 18th, 25th
Ans: D
Explanation: To find the day on 1st April 2001, we calculate the number of odd days from 1st January 2001 to 1st April 2001. Since 1st April 2001 is a Sunday, Wednesdays in April 2001 fall on the 4th, 11th, 18th, and 25th. - How many days are there in x weeks x days?
(A) 7x²
(B) 8x
(C) 14x
(D) 7
Ans: B
Explanation: x weeks and x days can be calculated as 7x+x=8x days. - The last day of a century cannot be:
(A) Monday
(B) Wednesday
(C) Tuesday
(D) Friday
Ans: C
Explanation: 100 years have 5 odd days, making the last day of the 1st century a Friday. Similarly, the last days of the 2nd, 3rd, and 4th centuries are Wednesday, Monday, and Sunday, respectively. Thus, the last day of a century cannot be Tuesday, Thursday, or Saturday. - On 8th Feb 2005 it was Tuesday. What was the day of the week on 8th Feb 2004?
(A) Tuesday
(B) Monday
(C) Sunday
(D) Wednesday
Ans: C
Explanation: The year 2004 is a leap year with 2 odd days. Therefore, the day on 8th Feb 2004 is 2 days before the day on 8th Feb 2005, which is a Tuesday. Hence, the day on 8th Feb 2004 was Sunday. - The product of two numbers is 4107. If the H.C.F. of these numbers is 37, then the greater number is:
(A) 101
(B) 107
(C) 111
(D) 185
Ans: C
Explanation:
Let the numbers be 37a and 37b.
Then, 37a×37b=4107, so ab=3.
The co-primes with product 3 are (1, 3).
Thus, the numbers are (37 × 1, 37 × 3), i.e., (37, 111).
Therefore, the greater number is 111. - Three numbers are in the ratio of 3 : 4 : 5 and their L.C.M. is 2400. Their H.C.F. is:
(A) 40
(B) 80
(C) 120
(D) 200
Ans: A
Explanation:
Let the numbers be 3x, 4x, and 5x.
Their L.C.M. is 60x.
Given, 60x=2400, so x=40.
Therefore, the numbers are 120, 160, and 200.
Hence, the required H.C.F. is 40. - The G.C.D. of 1.08, 0.36, and 0.9 is:
(A) 0.03
(B) 0.9
(C) 0.18
(D) 0.108
Ans: C
Explanation:
The numbers are 1.08, 0.36, and 0.90.
The H.C.F. of 108, 36, and 90 is 18.
Therefore, the H.C.F. of the given numbers is 0.18. - The product of two numbers is 2028 and their H.C.F. is 13. The number of such pairs is:
(A) 1
(B) 2
(C) 3
(D) 4
Ans: B
Explanation:
Let the numbers be 13a and 13b.
Then, 13a×13b=2028, so ab=12.
The co-primes with product 12 are (1, 12) and (3, 4).
Thus, the required numbers are (13 × 1, 13 × 12) and (13 × 3, 13 × 4).
Hence, there are 2 such pairs. - The least multiple of 7, which leaves a remainder of 4 when divided by 6, 9, 15, and 18, is:
(A) 74
(B) 94
(C) 184
(D) 364
Ans: D
Explanation:
The L.C.M. of 6, 9, 15, and 18 is 90.
Let the required number be 90k+4, which is a multiple of 7.
The least value of k for which 90k+4 is divisible by 7 is k=4.
Thus, the required number is 90×4+4=364. - Three pipes A, B, and C can fill a tank in 30 minutes, 20 minutes, and 10 minutes, respectively. After 3 minutes, what is the proportion of solution R in the tank?
(A) 5/11
(B) 6/11
(C) 7/11
(D) 8/11
Ans: B
Explanation: The part filled by A, B, and C together in 3 minutes is 11/20. The part filled by C alone in 3 minutes is 3/10. Hence, the required ratio of R = (3/10) * (20/11) = 6/11. - Pipes A and B can fill a tank in 5 and 6 hours respectively, and C can empty it in 12 hours. If all are opened, how long to fill the tank?
(A) 1 13/17 hours
(B) 2 8/11 hours
(C) 3 9/17 hours
(D) 4 1/2 hours
Ans: C
Explanation: Net part filled in 1 hour = 17/60. Therefore, the tank will be full in 60/17 hours, or 3 9/17 hours. - A pump can fill a tank in 2 hours, but due to a leak, it took 2.5 hours. The leak can drain all water in:
(A) 4 1/3 hours
(B) 7 hours
(C) 8 hours
(D) 14 hours
Ans: D
Explanation: Work done by the leak in 1 hour = 1/2 – 2/7 = 1/14. Thus, the leak will empty the tank in 14 hours. - Two pipes A and B can fill a cistern in 37 and 45 minutes. If B is turned off after a certain time, the cistern fills in 30 minutes. After how long is B turned off?
(A) 5 min
(B) 9 min
(C) 10 min
(D) 15 min
Ans: B
Explanation: Let B be turned off after x minutes. Then,
Part filled by (A + B) in x min. + Part filled by A in (30 -x) min. = 1
x(2/75+ 1/45)+ (30- x). 2/75=1
11x/225 + (60-2x)/ 75 = 1
11x + 180 – 6x = 225.
= x = 9. - A tank is filled by three pipes. The second pipe fills 5 hours faster than the first and 4 hours slower than the third. The time required by the first pipe is:
(A) 6 hours
(B) 10 hours
(C) 15 hours
(D) 30 hours
Ans: C
Explanation: 1/x+ 1/ (x – 5)= 1/ (x – 9)
2x – 5)(x – 9) = x(x – 5)
x2 – 18x + 45 = 0
(x – 15)(x – 3) = 0
x = 15





