Rational Numbers- Definition Symbol, and Examples

Rational Number

In Mathematics, Rational Numbers are is a type of number that can be represented in the form of p/q, where p and q can be any integer and q is not equal to zero. Thus, natural numbers, whole numbers, integers, fractions of integers, and decimals are all examples of rational numbers.  Let us know more about rational numbers, their types and properties, the difference between rational and irrational numbers, and examples in this article.

Rational Number Definition

A rational number is any number that can be expressed as p/q, where q is not equal to 0. In other words, any fraction that has an integer denominator and numerator and a denominator that is not zero fall into the category of rational numbers. Some Examples of Rational Numbers are 1/6, 2/4, 1/3,4/7, etc

Rational Number Meaning

Rational Number Meaning: The term “rational Number” is derived from the word “ratio” in mathematics. Therefore, it is simple to grasp how rational numbers connect to the idea of fractions, which stand for ratios.

A rational number that can be expressed as a fraction and has an integer denominator and numerator and one that is not zero is said to be rational. A rational number can therefore be written as p/q, where p and q are both integers and q ≠ 0.

Rational Numbers are Denoted by Symbol

Rational numbers are the set of numbers in which numbers can express in form of friction or p/q form, where p and q both are integers and q is not equal not zero. The set of a rational number is denoted by  Q, Look at the below image to get a clear idea of a rational Number,

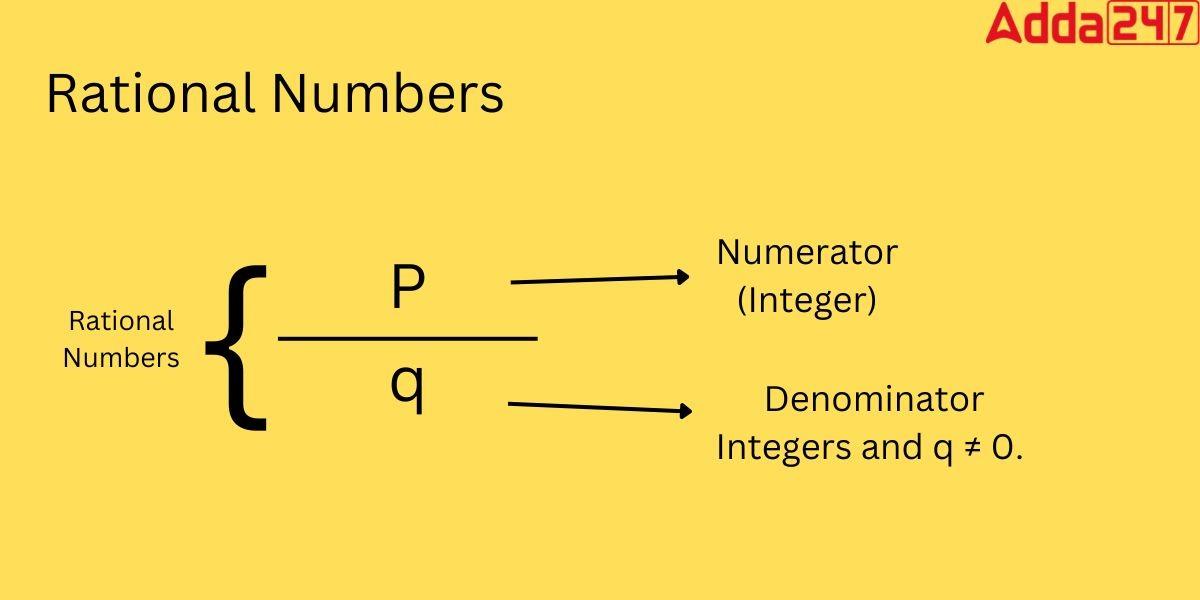
Rational Numbers Examples

We came to know that any number can be expressed in a fraction where both the numerator and denominator are integers and the denominator ≠ 0. Some Examples of Rational numbers are

• 0 (which is another form of 0/1)
• 1/3
• √25  is equal to 5
• -3/4
• 0.54 or 54/100
• -0.8 or -8/10
• 87 which can be written as 87/1
• 0.181818… or 18/99

Is 0 a rational Number?

Yes,0 is a Rational Number.Since it may be expressed as a fraction of an integer like 0/1, 0/-2, etc., 0 is a rational number. We have various ways to represent the number “0,” including 0/1, 0/2, 0/3, etc. However, /0, 2/0, 3/0, etc. are not rational,

Types of Rational Numbers

There are different types of Rational Numbers as follows

• Both Positive and negative integers are examples of rational numbers. For instance 2.-3,
• Rational numbers include fractions like 7/9, -3/5, etc. in which numerators and denominators are both integers, and the denominator is not equal to zero.
• Rational numbers include both types of decimals: 1) Terminating decimals, such as 0.89, 0.7656, and 0.345, etc which can be written in fractions.2)Non-terminating decimals with some repeating patterns, such as 0.666, 0.676767, etc.

Rational Numbers: Properties

The properties of Rational Numbers are

1. Rational numbers can express in form of friction or p/q form, where p and q both are integers and q is not equal not zero.
2. It is possible to represent the ratio p/q in decimal form, which is a further simplification.
3. A set of rational numbers includes zero, positive, and negative numbers.
4. Thus natural numbers, whole numbers, integers, fractions of integers, and decimals are all examples of rational numbers.

Arithmetic Operations on Rational Numbers

The fundamental operations we carry out on integers to solve a numerical problem in mathematics are called arithmetic operations. Here, let’s talk about how to carry out these operations on rational numbers. Consider two rational numbers.p/q and a/b.
Addition of Rational Number: To add two rational numbers, we must note that the denominator needs to be the same.
Hence in the addition of p/q and a/b.we obtain, (pb+qa)/qb.
For Example: 1/3+ 2/9 = (3+2)/9 = 5/9
Subtraction of Rational Numbers: In the Subtraction of two Rational Numbers, we must first make the denominator equal before doing the subtraction.
Hence in the Subtraction of p/q and a/b.we obtain, (pb-qa)/qb.
For Example:1/4 – 3/8 = (2-3)/8= -1/4

Multiplication and division of rational numbers: Rational numbers can be multiplied and divided in the same way as fractions. Any two rational integers can be multiplied by multiplying their numerators and denominators independently, then summing the resulting fraction. Let’s use an illustration to better grasp this.

Multiplication: If p/q is multiplied by a/b, then we obtain (p×a)/(q×b).

Example: 1/3 × 2/4 = (1×2)/(3×4) = 2/12=6

Division: If p/q is divided by a/b, then it is written as:
(p/q)÷(a/b) = pb/qa

Example: 1/3÷ 2/9 = (1×9)/(3×2) = 9/6 = 3/2=1.5

Rational Numbers list

Rational numbers are limitless in number. As a result, it is impossible to compile a complete list of rational numbers. This demonstrates that all decimals (including terminating decimals and recurring decimal numbers), whole numbers, integers, fractions, and decimals are thought to be rational numbers. For a better grasp of rational numbers, see the ven diagram below.

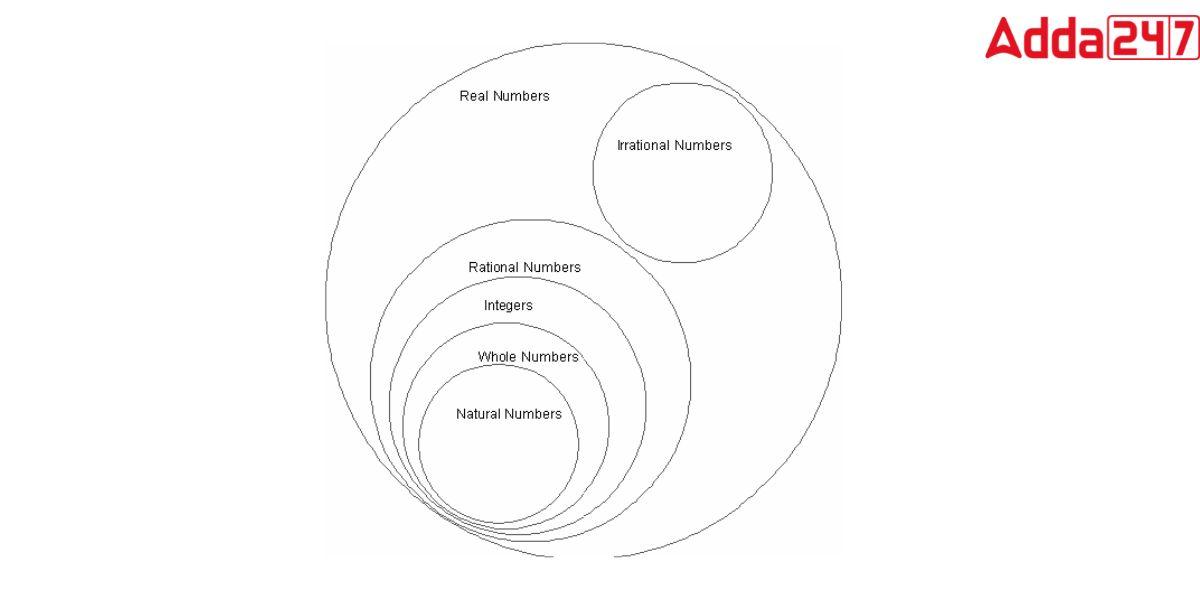
• All rational numbers are real numbers (R) (Q).
• The integers are a part of real numbers (Z).
• Natural numbers are a part of integers (N).
• All whole numbers are rational because they can all be expressed as fractions.

Rational Numbers and Irrational numbers: The Difference

Irrational numbers are those that ARE NOT rational numbers. The difference between rational and irrational numbers

Rational Numbers

In Math, rational numbers are a highly prevalent sort of number that students learn. These numbers are in the form p/q, where p and q are integers q ≠ 0.The Rational numbers are not as same as the fraction, there is a slight difference between the two. Whole numbers make up fractions, whereas integers make up the numerator and denominator of rational numbers.

The set of rational numbers also includes all integers, which can be expressed as a quotient with the integer as the numerator and 1 as the denominator. Rational numbers are either terminating or recurring decimals in decimal form. Irrational numbers are real numbers that cannot be written as a quotient of two integers.

Rational Numbers Definition

A rational number is a number that can be expressed as the quotient p/q of two numbers with q ≠ 0. The set of rational numbers also includes all integers, which can be expressed as a quotient with the integer as the numerator and 1 as the denominator. Rational numbers are either terminating or recurring decimals in decimal form. Irrational numbers are real numbers that cannot be written as a quotient of two integers.

Every Rational Numbers is a proper or improper fraction

In the same way that whole numbers and integers are represented on the number line, rational numbers can be represented on the number line. The number zero (0) is known as the origin on the number line. The positive values are shown on the right side of the origin, whereas the negative values are shown on the left. Let’s look at how to express rational numbers on a number line now.

There are two main sorts of representations for rational numbers. The rational number can be expressed as a proper or improper fraction.

Rational Numbers- Representation of a Proper Fraction

If it’s a proper fraction, the numerator is smaller than the denominator, so the supplied rational number should be less than 1 and more than 0, and we can simply express it on the number line.

Rational Numbers- Representation of a Improper Fraction

Because the numerator is bigger than the denominator in an improper fraction, the given rational number should be greater than 1. In this scenario, turn the improper fraction into a mixed fraction first. This conversion aids in determining the precise location of a given fraction on the number line. It’s useful to know where the fraction falls between two integers.

Rational Numbers more Examples

A rational number is one that can be written as a fraction with both the numerator and denominator being integers. Here are some examples of rational numbers:

1. -13, 0
2. 1/3
3. -3/7
4. 9 or 9/10
5. -0.01 or -1/100
6. 14/9

Is 0 a Rational number?

Yes, 0 (zero) is a rational number.

Rational Number in Hindi

परिमेय संख्या

गणित में, परिमेय संख्याएँ एक प्रकार की संख्याएँ होती हैं जिन्हें p/q के रूप में दर्शाया जा सकता है, जहाँ p और q कोई पूर्णांक हो सकते हैं और q शून्य के बराबर नहीं है। इस प्रकार, प्राकृतिक संख्याएँ, पूर्ण संख्याएँ, पूर्णांक, पूर्णांकों के अंश और दशमलव सभी परिमेय संख्याओं के उदाहरण हैं। आइए इस लेख में परिमेय संख्याओं, उनके प्रकार और गुणों, परिमेय और अपरिमेय संख्याओं के बीच के अंतर और उदाहरणों के बारे में अधिक जानें।

Rational Number ki Definition

एक परिमेय संख्या कोई भी संख्या है जिसे p/q के रूप में व्यक्त किया जा सकता है, जहाँ q 0 के बराबर नहीं है। दूसरे शब्दों में, कोई भी अंश जिसमें एक पूर्णांक भाजक और अंश और एक भाजक है जो शून्य नहीं है, परिमेय संख्याओं की श्रेणी में आता है। . परिमेय संख्याओं के कुछ उदाहरण 1/6, 2/4, 1/3,4/7, आदि हैं।

Rational Number Meaning in Hindi ( Rational Number Kya hote hai)

परिमेय संख्या का अर्थ: “तर्कसंगत संख्या” शब्द गणित में “अनुपात” शब्द से लिया गया है। इसलिए, यह समझना आसान है कि परिमेय संख्याएँ भिन्नों के विचार से कैसे जुड़ती हैं, जो अनुपातों के लिए खड़े होते हैं।

एक परिमेय संख्या जिसे भिन्न के रूप में व्यक्त किया जा सकता है और जिसमें एक पूर्णांक भाजक और अंश होता है और जो शून्य नहीं होता है, परिमेय संख्या कहलाती है। इसलिए एक परिमेय संख्या को p/q के रूप में लिखा जा सकता है, जहाँ p और q दोनों पूर्णांक हैं और q ≠ 0 है।

Rational Numbers-FAQs

Q.What is rational Numbers?

In Mathematics, Rational Numbers are a type of number that can be represented in the form of p/q, where p and q can be any integer and q is not equal to zero.

Q, How do you know if a number is rational?
A rational number is one that can be written as P/Q, where P and Q are both integers and Q is greater than zero. However, an irrational number cannot be expressed using simple fractions.

Q.Is 0 a rational Number?

Yes,0 is a Rational Number. Since it may be expressed as a fraction of an integer like 0/1, 0/-2, etc., 0 is a rational number. We have various ways to represent the number “0,” including 0/1, 0/2, 0/3, etc. However, /0, 2/0, 3/0, etc. are not rational.