Zero Polynomial Definition & Examples for Class 9, 10

Zero Polynomial Definition

A zero of a polynomial p(x) is the value of x for which the value of p(x) is 0. If k is a zero of p(x), then p(k)=0.

For example, consider a polynomial p(x)=x2−3x+2.

When x=1, the value of p(x) will be equal to

p(1)=12−3×1+2

=1−3+2

=0

Since p(x)=0 at x=1, we say that 1 is a zero of the polynomial x2−3x+2

Geometrical Meaning Of Zeros Of A Polynomial

A polynomial’s zeros are, geometrically speaking, the locations where its graph intersects the x-axis.

(i) One zero (Linear Polynomial)    (ii) Two zeros (Quadratic Polynomial)    (iii) Three zeros (Cubic Polynomial)

Here A, B and C correspond to the zeros of the polynomial represented by the graphs.

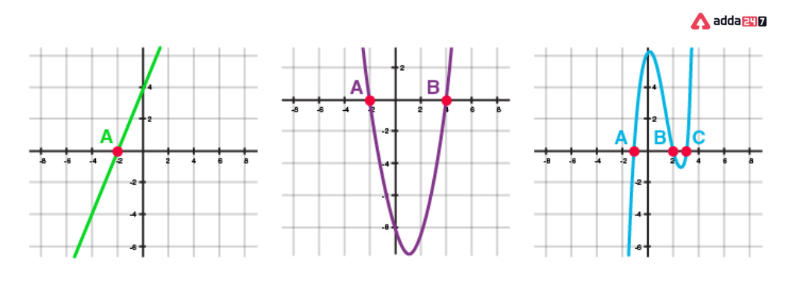
Number Of Zero Polynomial

A polynomial of degree n typically contains no more than n zeros.

• One zero exists in a linear polynomial.
• Maximum zeros in a quadratic polynomial are two.
• A cubic polynomial can only have three zero.

Ace your class 10th board exams with Adda247 live classes for class 10th preparation. 

Polynomials Factorisation

Quadratic polynomials can be factorized by splitting the middle term.

For example, consider the polynomial 2×2−5x+3

Splitting the middle term: The middle term in the polynomial 2×2−5x+3 is -5x. This must be expressed as a sum of two terms such that the product of their coefficients is equal to the product of 2 and 3 (coefficient of x2 and the constant term)

−5 can be expressed as (−2)+(−3), as −2×−3=6=2×3

Thus, 2×2−5x+3=2×2−2x−3x+3

Now, identify the common factors in individual groups

2×2−2x−3x+3=2x(x−1)−3(x−1)

Taking (x−1) as the common factor, this can be expressed as:

2x(x−1)−3(x−1)=(x−1)(2x−3)

Polynomial Division Algorithm

Let us assume that P(x) and G(x) are the two polynomials, such that G(x)≠ 0, then the division algorithm states the formula to find Q(x) and R(x) of the polynomial.

Here, P(x) denotes dividend polynomial

G(x) denotes divisor polynomial

Q(x) denotes quotient polynomial

R(x) denotes the remainder polynomial.

Thus, the formula stated by division algorithm is:

P(x) = G(x) × Q(x) + R(x)

Follow the instructions below to divide one polynomial by another.

Step 1: First, sort the terms of the dividend and the divisor according to decreasing degree.

Step 2: Subtract the highest degree term of the dividend from the highest degree term of the divisor to get the first term of the quotient. execute the division process after that.

Step 3: The payout for the following division is the leftovers from the previous division. Continue doing this until the remainder’s degree is lower than the divisor’s degree.

Polynomials for Class 9 and 10 Graphical Representation 

Here, let’s examine the graph representation of a polynomial equation.

Equation Representation On A Graph

Every point on the graph represents the x and y coordinates of the point that satisfies the equation, and any equation may be represented as a graph on the Cartesian plane. Any point that fulfils an equation will reside on the curve since an equation is only a constraint on the x and y coordinates of a point.

For instance, the straight line formed by the graph’s equation y = x will connect all the spots whose x and y coordinates are equal. For instance, (1,1), (2,2), and so forth.

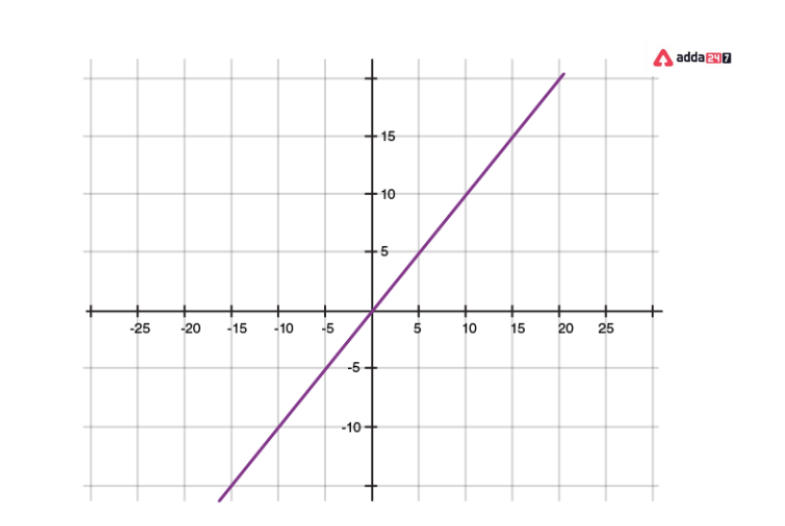
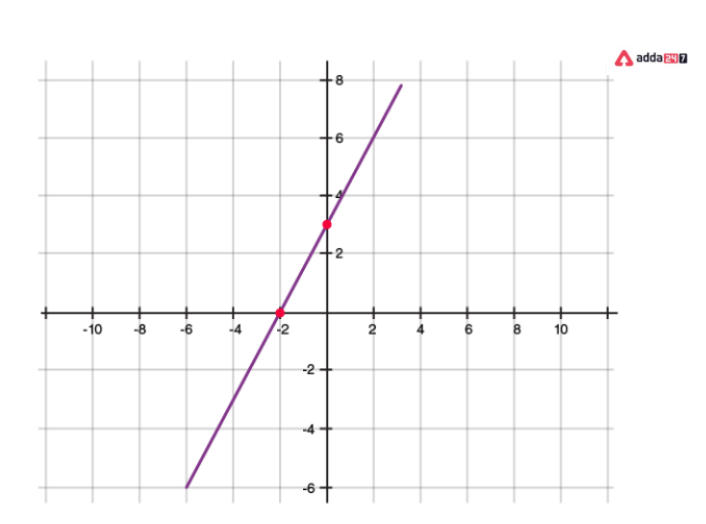
Geometrical Representation Of A Linear Polynomial

A linear polynomial has a straight line for its graph. It precisely cuts the X-axis at one place.

Geometrical Representation Of A Quadratic Polynomial

• A parabola is a quadratic polynomial’s graph.
• It resembles a U that, depending on the value of “a” in ax2+bx+c, either opens upwards or downwards.
• The parabola opens upwards if “a” is positive, and downwards if “a” is negative.
• The x-axis can be clipped at 0, 1, or two points.

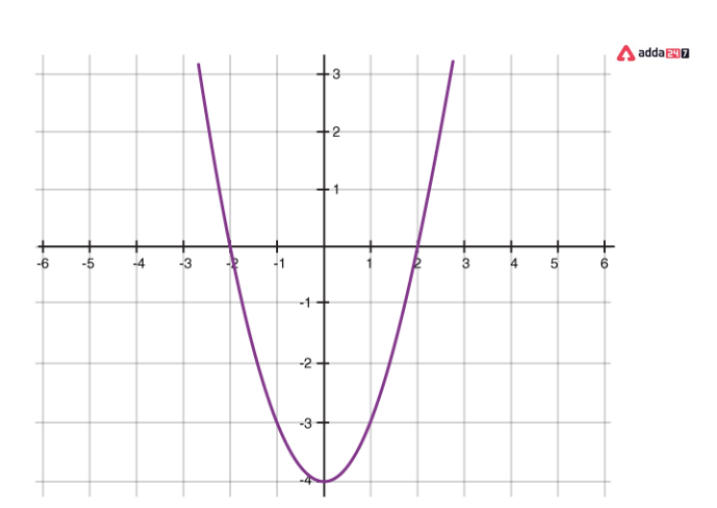
Graph of a polynomial which cuts the x-axis in two distinct points (a>0)

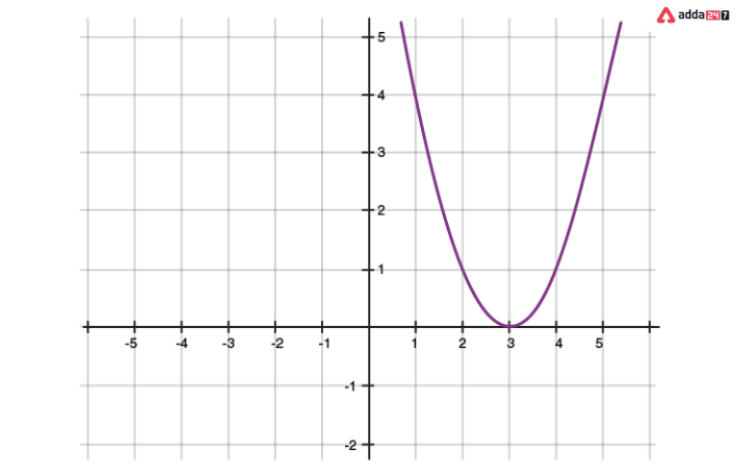
A graph of a quadratic polynomial with one point touching the x-axis (a>0)

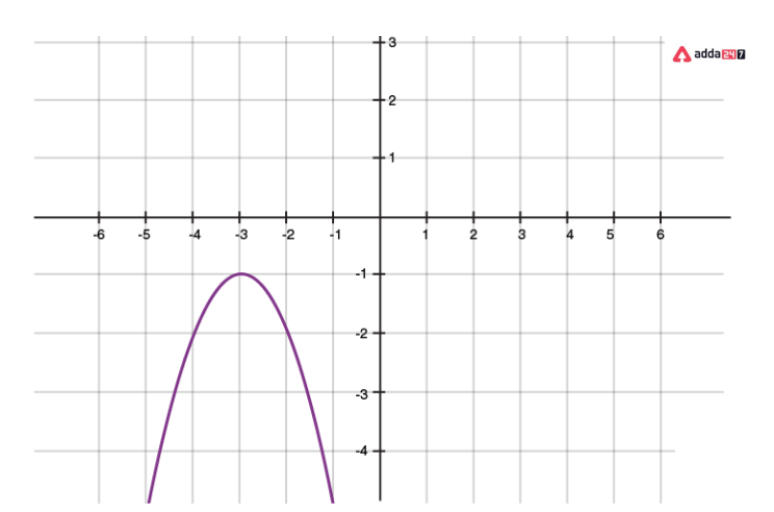
A quadratic polynomial’s (a<0) graph showing that it does not touch the x-axis.