Table of Contents
Class 12 Maths Important Questions
The students appearing in the CBSE Class 12 must solve the CBSE Class 12 Maths Important Questions given on this page. Mathematics requires practice, the more you practice maths questions your chances of getting good marks in Maths will increase. CBSE Class 12 Maths Important Questions are best to practice. We have provided the solutions to CBSE Class 12 Maths Important Questions. Bookmark this page to get all the updates from the Central Board of Secondary Education.
Class 12 Maths Important Questions With Solutions: 2 Marks
Q.1: Determine the principal value of cos-1( -1/2).
Solution:
Let us assume that, y = cos-1( -1/2)
We can write this as:
cos y =- 1/2
cos y = cos (2π/3).
Thus, the Range of the principal value of cos-1 is [0, π ].
Therefore, the principal value of cos-1( -1/2) is 2π /3.
Q.2: Find the value of cot (tan-1 α + cot-1 α).
Solution:
Given that: cot (tan-1 ? + cot-1 ?)
= cot (?/?) (since, tan-1 x + cot-1 x = ?/2)
= cot (180°/2) ( we know that cot 90° = 0 )
= cot (90°)
= 0
Therefore, the value of cot (tan-1 α + cot-1 α) is 0.
Q.3: The value of tan-1 √3 – sec-1(–2) is equal to:
(A) π (B) – π/3 (C) π/3 (D) 2π/3
Solution:
Now, solve the first part of the expression: tan-1 √3
Let us take y = tan-1√3
This can be written as:
tan y = √3
Now, use the trigonometry table to find the radian value
tan y = tan (π/3)
Thus, the range of principal value of tan-1 is (−π/2, π/2)
Therefore, the principal value of tan-1√3 is π/3.
Now, solve the second part of the expression: sec-1(–2)
Now, assume that y = sec-1 (–2)
sec y = -2
sec y = sec (2π/3)
We know that the principal value range of sec-1 is [0,π] – {π/2}
Therefore, the principal value of sec-1 (–2) = 2π/3
Now we have:
tan-1(√3) = π/3
sec-1 (–2) = 2π/3
Now, substitute the values in the given expression:
= tan-1 √3 – sec-1 (−2)
= π/3 − (2π/3)
= π/3 − 2π/3
= (π − 2π)/3
= – π/3
Hence, the correct answer is an option (B)
Q.4: Prove that sin-1 (3/5) – sin-1 (8/17) = cos-1 (84/85).
Solution:
Let sin-1 (3/5) = a and sin-1 (8/17) = b
Thus, we can write sin a = 3/5 and sin b = 8/17
Now, find the value of cos a and cos b
To find cos a:
Cos a = √[1 – sin2 a]
= √[1 – (3/5)2 ]
= √[1 – (9/25)]
= √[(25-9)/25]
= 4/5
Thus, the value of cos a = 4/5
To find cos b:
Cos b= √[1 – sin2 b]
= √[1 – (8/17)2 ]
= √[1 – (64/289)]
= √[(289-64)/289]
= 15/17
Thus, the value of cos b = 15/17
We know that cos (a- b) = cos a cos b + sin a sin b
Now, substitute the values for cos a, cos b, sin a and sin b in the formula, we get:
cos (a – b) = (4/5)x (15/17) + (3/5)x(8/17)
cos (a – b) = (60 + 24)/(17x 5)
cos (a – b) = 84/85
(a – b) = cos-1 (84/85)
Substituting the values of a and b sin-1 (3/5)- sin-1 (8/7) = cos-1 (84/85)
Hence proved.
Q. 5: Find the value of cos-1 (1/2) + 2 sin-1 (1/2).
Solution:
First, solve for cos-1 (1/2):
Let us take, y = cos-1 (1/2)
This can be written as:
cos y = (1/2)
cos y = cos (π /3).
Thus, the range of principal value of cos-1 is [0, π ]
Therefore, the principal value of cos-1 (1/2) is π/3.
Now, solve for sin-1 (1/2):
Let y = sin-1 (1/2)
sin y = 1/2
sin y = sin ( π/6)
Thus, the range of principal value of sin-1 is [(-π)/2, π/2 ]
Hence, the principal value of sin-1 (1/2) is π/6.
Now we have cos-1 (1/2) = π/3 & sin-1 (1/2) = π/6
Now, substitute the obtained values in the given formula, we get:
= cos-1 (1/2) + 2sin-1 (1/2)
= π /3 + 2( π/6)
= π/3 + π/3
= ( π+π )/3
= 2π /3
Thus, the value of cos-1 (1/2) + 2 sin-1 (1/2) is 2π /3.
Q. 6: Find the direction cosines of the line passing through the two points (– 2, 4, – 5) and (1, 2, 3).
Solution:
We know that the direction cosines of the line passing through two points P(x1, y1, z1) and Q(x2, y2, z2) are given by
Using the distance formula,
From the given,
P(x1, y1, z1) = (-2, 4, -5) and Q(x2, y2, z2) = (1, 2, 3)
Hence, the direction cosines of the line joining the given two points are.
Q. 7: Show that the points A (2, 3, – 4), B (1, – 2, 3) and C (3, 8, – 11) are collinear.
Solution:
We know that the direction ratios of the line passing through two points P(x1, y1, z1) and Q(x2, y2, z2) are given by:
x2 – x1, y2 – y1, z2 – z1 or x1 – x2, y1 – y2, z1 – z2
Given points are A (2, 3, – 4), B (1, – 2, 3) and C (3, 8, – 11).
Direction ratios of the line joining A and B are:
1 – 2, – 2 – 3, 3 + 4
i.e. – 1, – 5, 7.
The direction ratios of the line joining B and C are:
3 –1, 8 + 2, – 11 – 3
i.e., 2, 10, – 14.
From the above, it is clear that direction ratios of AB and BC are proportional.
That means AB is parallel to BC. But point B is common to both AB and BC.
Hence, A, B, C are collinear points.
Q. 8: If a line makes angles 90°, 135°, 45° with the x, y and z-axes respectively, find its direction cosines.
Solution:
Let the direction cosines of the line be l, m, and n.
l = cos 90° = 0
m = cos 135° = -1/√2
n = cos 45° = 1/√2
Hence, the direction cosines of the line are 0, -1/√2, and 1/√2.
Q. 9: Find the angle between the pair of lines given by
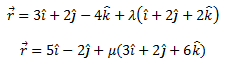
Solution:
From the given,
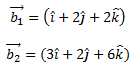
Let θ be the angle between the given pair of lines.
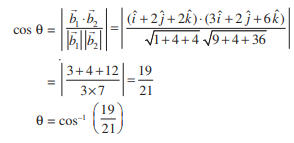
Q. 10: Find the angle between the pair of lines given below.
(x + 3)/3 = (y -1)/5 = (z + 3)/4
(x + 1)/1 = (y – 4)/1 = (z – 5)/2
Solution:
Given,
(x + 3)/3 = (y -1)/5 = (z + 3)/4
(x + 1)/1 = (y – 4)/1 = (z – 5)/2
The direction ratios of the first line are:
a1 = 3, b1 = 5, c1 = 4
The direction ratios of the second line are:
a2 = 1, b2 = 1, c2 = 2
Hence, the required angle is
Q. 11: Find the distance between the lines l1 and l2 given by:
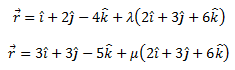
Solution:
Given two lines are parallel.
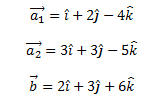
The distance between the two given lines is
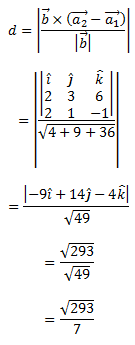
Q. 12: Show that the lines (x – 5)/7 = (y + 2)/-5 = z/1 and x/1 = y/2 = z/3 are perpendicular to each other.
Solution:
Given lines are:
(x – 5)/7 = (y + 2)/-5 = z/1 and x/1 = y/2 = z/3
The direction ratios of the given lines are 7, -5, 1 and 1, 2, 3, respectively.
We know that,
Two lines with direction ratios a1, b1, c1 and a2, b2, c2 are perpendicular to each other if a1a2 + b1b2 + c1c2 = 0
Therefore, 7(1) + (-5) (2) + 1 (3)
= 7 – 10 + 3
=0
Hence, the given lines are perpendicular to each other.
Q. 13: Find the vector equation of a plane which is at a distance of 7 units from the origin and normal to the vector
Solution:
Given, the normal vector is:
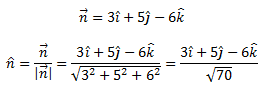
We know that the equation of the plane with position vector is given by
Hence, the vector equation of the required plane is
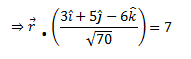
Q. 14: Find the intercepts cut off by the plane 2x + y – z = 5.
Solution:
Given plane is 2x + y – z = 5 ……(i)
Dividing both sides of the equation (i) by 5,
(⅖)x + (y/5) – (z/5) = 1
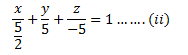
We know that,
The equation of a plane in intercept form is (x/a) + (y/b) + (z/c) = 1, where a, b, c are intercepts cut off by the plane at x, y, z-axes respectively.
For the given equation,
a = 5/2, b = 5, c = -5
Hence, the intercepts cut off by the plane are 5/2, 5 and -5.
Q. 15: Find the equations of the planes that passes through three points (1, 1, 0), (1, 2, 1), and (– 2, 2, – 1).
Solution:
Given points are (1, 1, 0), (1, 2, 1), and (– 2, 2, – 1).
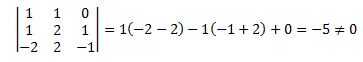
Therefore, the plane will pass through the given three points.
We know that,
The equation of the plane through the points (x1, y1, z1), (x2, y2, z2) and (x3, y3, z3) is
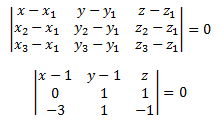
(x – 1)(-2) -(y – 1) (3) + z (3) = 0
-2x + 2 – 3y + 3 + 3z = 0
-2x – 3y + 3z + 5 = 0
-2x – 3y + 3z = -5
Therefore, 2x + 3y – 3z = 5 is the required Cartesian equation of the plane.
Q. No.16: Determine order and degree (if defined) of differential equation (y′′′)2 + (y″)3 + (y′)4 + y5 = 0
Solution:
Given differential equation is (y′′′)2 + (y″)3 + (y′)4 + y5 = 0
The highest order derivative present in the differential equation is y′′′.
Therefore, its order is 3.
The given differential equation is a polynomial equation in y′′′, y′′, and y′.
The highest power raised to y′′′ is 2.
Hence, its degree is 2.
Q. No. 17: Verify that the function y = a cos x + b sin x, where, a, b ∈ R is a solution of the differential equation d2y/dx2 + y=0.
Solution:
The given function is y = a cos x + b sin x … (1)
Differentiating both sides of equation (1) with respect to x,
dy/dx = – a sinx + b cos x
d2y/dx2 = – a cos x – b sinx
LHS = d2y/dx2 + y
= – a cos x – b sinx + a cos x + b sin x
= 0
= RHS
Hence, the given function is a solution to the given differential equation.
Q. No. 18: The number of arbitrary constants in the general solution of a differential equation of fourth order is:
(A) 0 (B) 2 (C) 3 (D) 4
Solution:
We know that the number of constants in the general solution of a differential equation of order n is equal to its order.
Therefore, the number of constants in the general equation of the fourth-order differential equation is four.
Hence, the correct answer is D.
Note: The number of constants in the general solution of a differential equation of order n is equal to zero.
Q. No. 19: Form the differential equation representing the family of curves y = a sin (x + b), where a, b are arbitrary constants.
Solution:
Given,
y = a sin (x + b) … (1)
Differentiating both sides of equation (1) with respect to x,
dy/dx = a cos (x + b) … (2)
Differentiating again on both sides with respect to x,
d2y/dx2 = – a sin (x + b) … (3)
Eliminating a and b from equations (1), (2) and (3),
d2y/ dx2 + y = 0 … (4)
The above equation is free from the arbitrary constants a and b.
This the required differential equation.
Important Questions For Class 12 Maths With Solutions: 3 Marks
Q. No. 1 Find the differential equation of the family of lines through the origin.
Solution:
Let y = mx be the family of lines through the origin.
Therefore, dy/dx = m
Eliminating m, (substituting m = y/x)
y = (dy/dx) . x
or
x. dy/dx – y = 0
Q. No. 2: Form the differential equation of the family of circles having a centre on y-axis and radius 3 units.
Solution:
The general equation of the family of circles having a centre on the y-axis is x2 + (y – b)2 = r2
Given the radius of the circle is 3 units.
The differential; equation of the family of circles having a centre on the y-axis and radius 3 units is as below:
x2 + (y – b)2 = 32
x2 + (y – b)2 = 9 ……(i)
Differentiating (i) with respect to x,
2x + 2(y – b).y′ = 0
⇒ (y – b). y′ = -x
⇒ (y – b) = -x/y′ …….(ii)
Substituting (ii) in (i),
x2 + (-x/y′)2 = 9
⇒ x2[1 + 1/(y′)2] = 9
⇒ x2 [(y′)2 + 1) = 9 (y′)2
⇒ (x2 – 9) (y′)2 + x2 = 0
Hence, this is the required differential equation.
Q. No. 3: Find the general solution of the differential equation dy/dx =1+y2/1+x2.
Solution:
Given differential equation is dy/dx =1+y2/1+x2
Since 1 + y2 ≠ 0, therefore by separating the variables, the given differential equation can be written as:
dy/1+y2 = dx/1+x2 …….(i)
Integrating equation (i) on both sides,
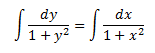
tan-1y = tan-1x + C
This is the general solution of the given differential equation.
Q. No. 4: For each of the given differential equation, find a particular solution satisfying the given condition:
dy/dx = y tan x ; y = 1 when x = 0
Solution:
dy/dx = y tan x
dy/y = tan x dx
Integrating on both sides,
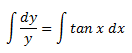
log y = log (sec x) +C
log y = log (C sec x)
⇒ y = C sec x ……..(i)
Now consider y = 1 when x= 0.
1 = C sec 0
1 = C (1)
C = 1
Substituting C = 1 in (i)
y = sec x
Hence, this is the required particular solution of the given differential equation.
Q. No. 5: Find the equation of a curve passing through (1, π/4) if the slope of the tangent to the curve at any point P (x, y) is y/x – cos2(y/x).
Solution:
According to the given condition,
dy/dx = y/x – cos2(y/x) ………….(i)
This is a homogeneous differential equation.
Substituting y = vx in (i),
v + (x) dv/dx = v – cos2v
⇒ (x)dv/dx = – cos2v
⇒ sec2v dv = – dx/x
By integrating on both the sides,
⇒ ∫sec2v dv = – ∫dx/x
⇒ tan v = – log x + c
⇒ tan (y/x) + log x = c ……….(ii)
Substituting x = 1 and y = π/4,
⇒ tan (π/4) + log 1 = c
⇒ 1 + 0 = c
⇒ c = 1
Substituting c = 1 in (ii),
tan (y/x) + log x = 1
Q. No. 6: Integrating factor of the differential equation (1 – x2)dy/dx – xy = 1 is
(A) -x
(B) x/ (1 + x2)
(C) √(1- x2)
(D) ½ log (1 – x2)
Solution:
Given differential equation is (1 – x2)dy/dx – xy = 1
(1 – x2)dy/dx = 1 + xy
dy/dx = (1/1 – x2) + (x/1 – x2)y
dy/dx – (x/1 – x2)y = 1/1-x2
This is of the form dy/dx + Py = Q
We can get the integrating factor as below:
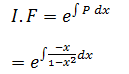
Let 1 – x2 = t
Differentiating with respect to x
-2x dx = dt
-x dx = dt/2
Now,
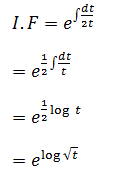
I.F = √t = √(1- x2)
Hence, option C is the correct answer.
Question 7:
Evaluate: ∫ 3ax/(b2 +c2x2) dx
Solution:
To evaluate the integral, I = ∫ 3ax/(b2 +c2x2) dx
Let us take v = b2 +c2x2, then
dv = 2c2x dx
Thus, ∫ 3ax/(b2 +c2x2) dx
= (3ax/2c2x)∫dv/v
Now, cancel x on both numerator and denominator, we get
= (3a/2c2)∫dv/v
= (3a/2c2) log |b2 +c2x2| + C
Where C is an arbitrary constant
Question 8:
Determine ∫tan8x sec4 x dx
Solution:
Given: ∫tan8x sec4 x dx
Let I = ∫tan8x sec4 x dx — (1)
Now, split sec4x = (sec2x) (sec2x)
Now, substitute in (1)
I = ∫tan8x (sec2x) (sec2x) dx
= ∫tan8x (tan2 x +1) (sec2x) dx
It can be written as:
= ∫tan10x sec2 x dx + ∫tan8x sec2 x dx
Now, integrate the terms with respect to x, we get:
I =( tan11 x /11) + ( tan9 x /9) + C
Hence, ∫tan8x sec4 x dx = ( tan11 x /11) + ( tan9 x /9) + C
Question 9:
Write the anti-derivative of the following function: 3x2+4x3
Solution:
Given: 3x2+4x3
The antiderivative of the given function is written as:
∫3x2+4x3 dx = 3(x3/3) + 4(x4/4)
= x3 + x4
Thus, the antiderivative of 3x2+4x3 = x3 + x4
Question 10:
Determine the antiderivative F of “f” , which is defined by f (x) = 4x3 – 6, where F (0) = 3
Solution:
Given function: f (x) = 4x3 – 6
Now, integrate the function:
∫4x3 – 6 dx = 4(x4/4)-6x + C
∫4x3 – 6 dx = x4 – 6x + C
Thus, the antiderivative of the function, F is x4 – 6x + C, where C is a constant
Also, given that, F(0) = 3,
Now, substitute x = 0 in the obtained antiderivative function, we get:
(0)4 – 6(0) + C = 3
Therefore, C = 3.
Now, substitute C = 3 in antiderivative function
Hence, the required antiderivative function is x4 – 6x + 3.
Question 11:
Integrate the given function using integration by substitution: 2x sin(x2+ 1) with respect to x:
Solution:
Given function: 2x sin(x2+ 1)
We know that, the derivative of x2 + 1 is 2x.
Now, use the substitution method, we get
x2 + 1 = t, so that 2x dx = dt.
Hence, we get ∫ 2x sin ( x2 +1) dx = ∫ sint dt
= – cos t + C
= – cos (x2 + 1) + C
Where C is an arbitrary constant
Therefore, the antiderivative of 2x sin(x2+ 1) using integration by substitution method is = – cos (x2 + 1) + C
Question 12:
Integrate: ∫ sin3 x cos2x dx
Solution:
Given that, ∫ sin3 x cos2x dx
This can be written as:
∫ sin3 x cos2x dx = ∫ sin2 x cos2x (sin x) dx
=∫(1 – cos2x ) cos2x (sin x) dx —(1)
Now, substitute t = cos x,
Then dt = -sin x dx
Now, equation can be written as:
Thus, ∫ sin3 x cos2x dx = – ∫ (1-t2)t2 dt
Now, multiply t2 inside the bracket, we get
= – ∫ (t2-t4) dt
Now, integrate the above function:
= – [(t3/3) – (t5/5)] + C —(2)
Where C is a constant
Now, substitute t = cos x in (2)
= -(⅓)cos3x +(1/5)cos5x + C
Hence, ∫ sin3 x cos2x dx = -(⅓)cos3x +(1/5)cos5x + C
Q. No.:13 Find the area enclosed by the ellipse x2/a2 + y2/b2 =1.
Solution:
Given,
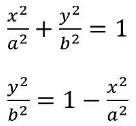
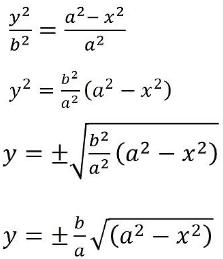
We know that,
Ellipse is symmetrical about both x-axis and y-axis.
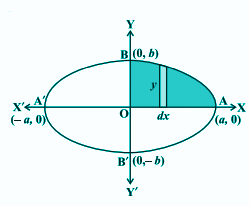
Area of ellipse = 4 × Area of AOB
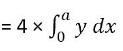
Substituting the positive value of y in the above expression since OAB lies in the first quadrant.
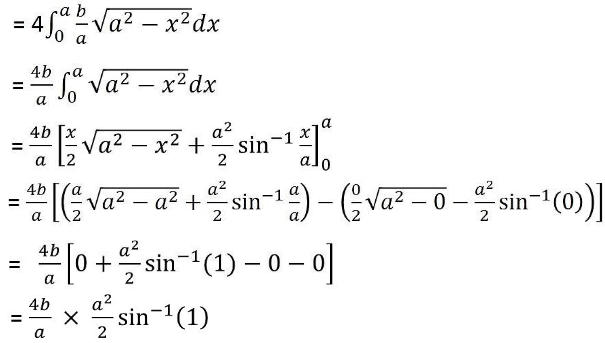
= 2ab × sin-1(1)
= 2ab × π/2
= πab
Hence, the required area is πab sq.units.
Important Questions For Class 12 Maths With Solutions: 4 Marks
Q. No. 1: Find the area of the region bounded by y2 = 9x, x = 2, x = 4 and the x-axis in the first quadrant.
Solution:
We can draw the figure of y2 = 9x; x = 2, x = 4 and the x-axis in the first curve as below.
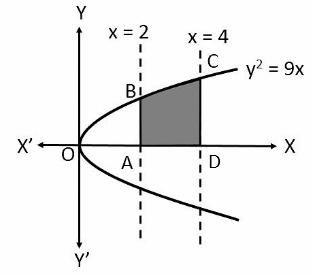
y2 = 9x
y = ±√(9x)
y = ±3√x
We can consider the positive value of y since the required area is in the first quadrant.
The required area is the shaded region enclosed by ABCD.
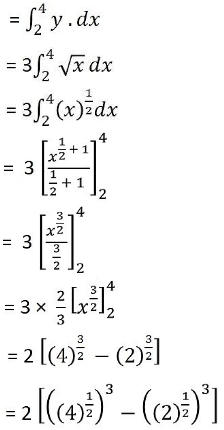
= 2 [(2)3 – (√2)3]
= 2[8 – 2√2]
= 16 – 4√2
Hence, the required area is 16 – 4√2 sq.units.
Q. No. 2: Find the area of the curve y = sin x between 0 and π.
Solution:
Given,
y = sin x
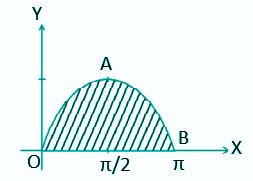
Area of OAB
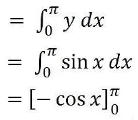
= – [cos π – cos 0]
= -(-1 -1)
= 2 sq. units
Q. No. 3: Find the area of the region bounded by the two parabolas y = x2 and y2 = x.
Solution:
Given two parabolas are y = x2 and y2 = x.
The point of intersection of these two parabolas is O (0, 0) and A (1, 1) as shown in the below figure.
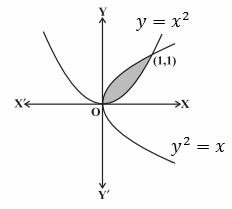
Now,
y2 = x
y = √x = f(x)
y = x2 = g(x), where, f (x) ≥ g (x) in [0, 1].
Area of the shaded region
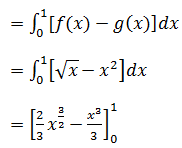
= (⅔) – (⅓)
= ⅓
Hence, the required area is ⅓ sq.units.
Q. No. 4: Smaller area enclosed by the circle x2+ y2 = 4 and the line x + y = 2 is
(A) 2 (π – 2)
(B) π – 2
(C) 2π – 1
(D) 2 (π + 2)
Solution:
Option (B) is the correct answer.
Explanation:
Given,
Equation of circle is x2+ y2 = 4……….(i)
x2+ y2 = 22
y = √(22 – x2) …………(ii)
Equation of a lines is x + y = 2 ………(iii)
y = 2 – x
| x | 0 | 2 |
| y | 2 | 0 |
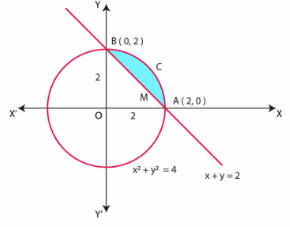
Therefore, the graph of equation (iii) is the straight line joining the points (0, 2) and (2, 0).
From the graph of a circle (i) and straight-line (iii), it is clear that points of intersections of circle
(i) and the straight line (iii) is A (2, 0) and B (0.2).
Area of OACB, bounded by the circle and the coordinate axes is
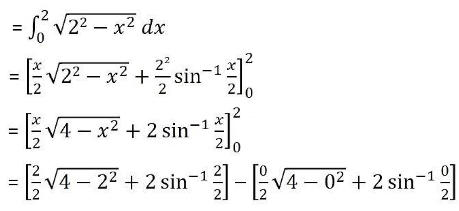
= [ 1 × √0 + 2 sin-1(1) – 0√4 – 2 × 0]
= 2 sin-1(1)
= 2 × π/2
= π sq. units
Area of triangle OAB, bounded by the straight line and the coordinate axes is
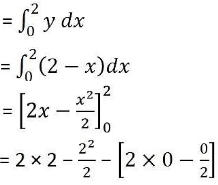
= 4 – 2 – 0 + 0
= 2 sq.units
Hence, the required area = Area of OACB – Area of triangle OAB
= (π – 2) sq.units
Question 5:
Explain the continuity of the function f(x) = sin x . cos x
Solution:
We know that sin x and cos x are continuous functions. It is known that the product of two continuous functions is also a continuous function.
Hence, the function f(x) = sin x . cos x is a continuous function.
Question 6:
Determine the points of discontinuity of the composite function y = f[f(x)], given that, f(x) = 1/x-1.
Solution:
Given that, f(x) = 1/x-1
We know that the function f(x) = 1/x-1 is discontinuous at x = 1
Now, for x ≠1,
f[f(x)]= f(1/x-1)
= 1/[(1/x-1)-1]
= x-1/ 2-x, which is discontinuous at the point x = 2.
Therefore, the points of discontinuity are x = 1 and x=2.
Question 7:
If f (x) = |cos x|, find f’(3π/4)
Solution:
Given that, f(x) = |cos x|
When π/2 <x< π, cos x < 0,
Thus, |cos x| = -cos x
It means that, f(x) = -cos x
Hence, f’(x) = sin x
Therefore, f’(3π/4) = sin (3π/4) = 1/√2
f’(3π/4) = 1/√2
Question 8:
Verify the mean value theorem for the following function f (x) = (x – 3) (x – 6) (x – 9) in [3, 5]
Solution:
f(x)=(x−3)(x−6)(x−9)
=(x−3)(x2−15x+54)
=x3−18x2+99x−162
fc∈(3,5)
f′(c)=f(5)−f(3)/5−3
f(5)=(5−3)(5−6)(5−9)
=2(−1)(−4)=−8
f(3)=(3−3)(3−6)(3−9)=0
f′(c)=8−0/2=4
∴f′(c)=3c2−36c+99
3c2−36c+99=4
3c2−36c+95=0
ax2+bx+c=0
a=3
b=−36
c=95
c=36±√(36)2−4(3)(95)/2(3)
=36±√1296−1140/6
=36±12.496
c=8.8&c=4.8
c∈(3,5)
f(x)=(x−3)(x−6)(x−9) on [3,5]
Question 9:
Explain the continuity of the function f = |x| at x = 0.
Solution:
From the given function, we define that,
f(x) = {-x, if x<0 and x, if x≥0
It is clearly mentioned that the function is defined at 0 and f(0) = 0. Then the left-hand limit of f at 0 is
Limx→0- f(x)= limx→0- (-x) = 0
Similarly for the right hand side,
Limx→0+ f(x)= limx→0+ (x) = 0
Therefore, for the both left hand and the right hand limit, the value of the function coincide at the point x = 0.
Therefore, the function f is continuous at the point x =0.
Question 10:
If y= tan x + sec x , then show that d2.y / dx2 = cos x / (1-sin x)2
Solution:
Given that, y= tan x + sec x
Now, the differentiate wih respect to x, we get
dy/dx = sec2 x + sec x tan x
= (1/ cos2 x) + (sin x/ cos2 x)
= (1+sinx)/ (1+sinx)(1-sin x)
Thus, we get.
dy/dx = 1/(1-sin x)
Now, again differentiate with respect to x, we will get
d2y / dx2 = -(-cosx )/(1- sin x)2
d2y / dx2 = cos x / (1-sinx)2.
Q.11: Show that the Signum Function f: R → R, given by
Solution:
Check for one to one function:
For example:
f(0) = 0
f(-1) = -1
f(1) = 1
f(2) = 1
f(3) = 1
Since, for the different elements say f(1), f(2) and f(3), it shows the same image, then the function is not one to one function.
Check for Onto Function:
For the function,f: R →R
In this case, the value of f(x) is defined only if x is 1, 0, -1
For any other real numbers(for example y = 2, y = 100) there is no corresponding element x.
Thus, the function “f” is not onto function.
Hence, the given function “f” is neither one-one nor onto.
Q.12: If f: R → R is defined by f(x) = x2 − 3x + 2, find f(f(x)).
Solution:
Given function:
f(x) = x2 − 3x + 2.
To find f(f(x))
f(f(x)) = f(x)2 − 3f(x) + 2.
= (x2 – 3x + 2)2 – 3(x2 – 3x + 2) + 2
By using the formula (a-b+c)2 = a2+ b2+ c2-2ab +2ac-2ab, we get
= (x2)2 + (3x)2 + 22– 2x2 (3x) + 2x2(2) – 2x2(3x) – 3(x2 – 3x + 2) + 2
Now, substitute the values
= x4 + 9x2 + 4 – 6x3 – 12x + 4x2 – 3x2 + 9x – 6 + 2
= x4 – 6x3 + 9x2 + 4x2 – 3x2 – 12x + 9x – 6 + 2 + 4
Simplify the expression, we get,
f(f(x)) = x4 – 6x3 + 10x2 – 3x
Q.13: Let A = N × N and * be the binary operation on A defined by (a, b) * (c, d) = (a + c, b + d). Show that * is commutative and associative. Find the identity element for * on A, if any.
Solution:
Check the binary operation * is commutative :
We know that, * is commutative if (a, b) * (c, d) = (c, d) * (a, b) ∀ a, b, c, d ∈ R
L.H.S =(a, b) * (c, d)
=(a + c, b + d)
R. H. S = (c, d) * (a, b)
=(a + c, b + d)
Hence, L.H.S = R. H. S
Since (a, b) * (c, d) = (c, d) * (a, b) ∀ a, b, c, d ∈ R
* is commutative (a, b) * (c, d) = (a + c, b + d)
Check the binary operation * is associative :
We know that * is associative if (a, b) * ( (c, d) * (x, y) ) = ((a, b) * (c, d)) * (x, y) ∀ a, b, c, d, x, y ∈ R
L.H.S = (a, b) * ( (c, d) * (x, y) ) = (a+c+x, b+d+y)
R.H.S = ((a, b) * (c, d)) * (x, y) = (a+c+x, b+d+y)
Thus, L.H.S = R.H.S
Since (a, b) * ( (c, d) * (x, y) ) = ((a, b) * (c, d)) * (x, y) ∀ a, b, c, d, x, y ∈ R
Thus, the binary operation * is associative
Checking for Identity Element:
e is identity of * if (a, b) * e = e * (a, b) = (a, b)
where e = (x, y)
Thus, (a, b) * (x, y) = (x, y) * (a, b) = (a, b) (a + x, b + y)
= (x + a , b + y) = (a, b)
Now, (a + x, b + y) = (a, b)
Now comparing these, we get:
a+x = a
x = a -a = 0
Next compare: b +y = b
y = b-b = 0
Since A = N x N, where x and y are the natural numbers. But in this case, x and y is not a natural number. Thus, the identity element does not exist.
Therefore, the operation * does not have any identity element.
Q.14: Let f : N → Y be a function defined as f (x) = 4x + 3, where, Y = {y ∈ N: y = 4x + 3 for some x ∈ N}. Show that f is invertible. Find the inverse.
Solution:
Checking for Inverse:
f(x) = 4x + 3
Let f(x) = y
y = 4x + 3
y – 3 = 4x
4x = y – 3
x = (? − 3)/4
Let g(y) = (? − 3)/4
where g: Y → N
Now find gof:
gof= g(f(x))
= g(4x + 3) = [(4? + 3) − 3]/4
= [4? + 3 − 3]/4
=4x/4
= x = IN
Now find fog:
fog= f(g(y))
= f [(? − 3)/4]
=4[(? − 3)/4] +3
= y – 3 + 3
= y + 0
= y = Iy
Thus, gof = INand fog = Iy,
Hence, f is invertible
Also, the Inverse of f = g(y) = [? – 3]/ 4
Q. 15: Let A = R {3} and B = R – {1}. Consider the function f: A →B defined by f (x) = (x- 2)/(x -3). Is f one-one and onto? Justify your answer.
Solution:
Given function:
f (x) = (x- 2)/(x -3)
Checking for one-one function:
f (x1) = (x1– 2)/ (x1– 3)
f (x2) = (x2-2)/ (x2-3)
Putting f (x1) = f (x2)
(x1-2)/(x1-3)= (x2-2 )/(x2 -3)
(x1-2) (x2– 3) = (x1– 3) (x2-2)
x1 (x2– 3)- 2 (x2 -3) = x1 (x2– 2) – 3 (x2– 2)
x1 x2 -3x1 -2x2 + 6 = x1 x2 – 2x1 -3x2 + 6
-3x1– 2x2 =- 2x1 -3x2
3x2 -2x2 = – 2x1 + 3x1
x1= x2
Hence, if f (x1) = f (x2), then x1 = x2
Thus, the function f is one-one function.
Checking for onto function:
f (x) = (x-2)/(x-3)
Let f(x) = y such that y B i.e. y ∈ R – {1}
So, y = (x -2)/(x- 3)
y(x -3) = x- 2
xy -3y = x -2
xy – x = 3y-2
x (y -1) = 3y- 2
x = (3y -2) /(y-1)
For y = 1, x is not defined But it is given that. y ∈ R – {1}
Hence, x = (3y- 2)/(y- 1) ∈ R -{3} Hence, f is onto.
Related Post:
CBSE Class 12th Hindi Important Questions
CBSE Class 12th Biology Important Questions
CBSE Class 12th Chemistry Important Questions
CBSE Class 12th Physics Important Questions
CBSE Class 12th Maths Important Questions with Answer: QNA
Q. Is NCERT enough for Class 12 Term 2 Mathematics?
Yes, NCERT is more than enough for Class 12 Term 2 Mathematics. The students can practice the CBSE Class 12 Term 2 Mathematics Important Questions given on this page.
Q. Where can I find CBSE Class 12 Term 2 Mathematics Important Questions?
You can find the CBSE Class 12 Term 2 Mathematics Important Questions here. We have given the CBSE Class 12 Term 2 Mathematics Important Questions based on the latest CBSE Term 2 Exam pattern on this page.
Q. When CBSE will conduct the Class 12 Term 2 Exam for Mathematics?
The CBSE will conduct the Class 12 Term 2 Exam for Mathematics on the 7th of June 2022, Tuesday.


 JAC 11th Result 2024 Releasing on this D...
JAC 11th Result 2024 Releasing on this D...
 TN 11th Result 2024 to be Announced on M...
TN 11th Result 2024 to be Announced on M...
 VITEEE Sample Paper 2024, Download Subje...
VITEEE Sample Paper 2024, Download Subje...














